Суперпозиция колебаний с эквидистантными частотами

Пусть происходит N колебаний одинаковой амплитуды E ₀, частота которых различается на dw. Результат суперпозиции этих колебаний представляется формулой: .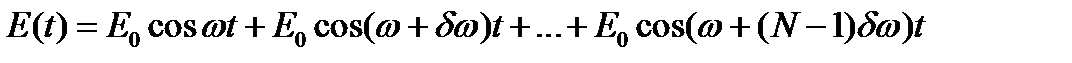

Суммирование этого ряда можно произвести в экспоненциальном представлении гармонических функций:

,

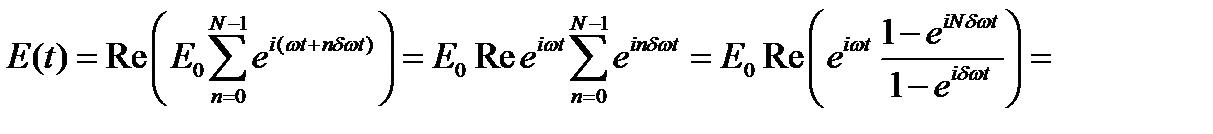
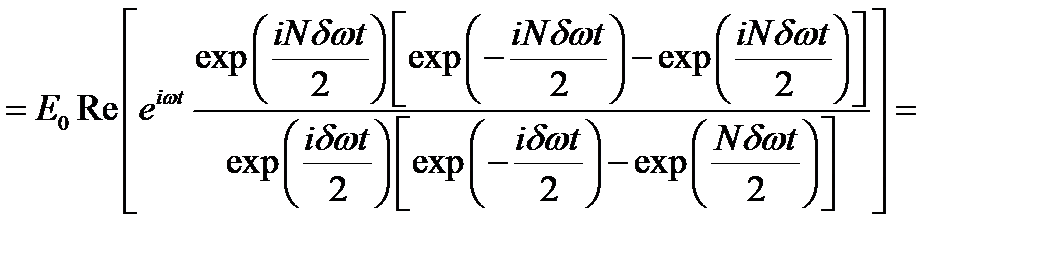
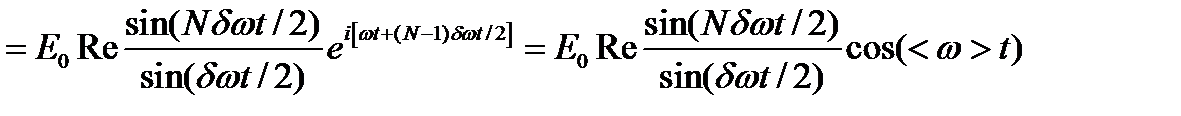где < w > = w + (N – 1) dw /2 - средняя частота волнового пакета.

Принимая во внимание, что Ndw = D w – полная ширина частот волнового пакета, выражение можно представить в виде .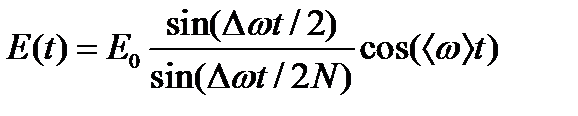

Р и с. 2.13

В большинстве случаев, представляющих практический интерес, 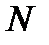>>1 и поэтому в течение многих периодов изменения аргумента D wt /2 у синуса в числителе формулы аргумент у синуса в знаменателе формулы остаeтся малым (D wt / 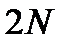<<1), так что можно считать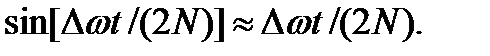

Поэтому можно записать в виде

.

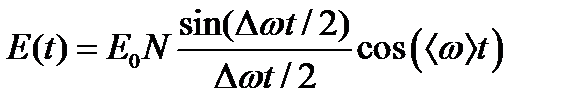График этой функции приведeн на рис. 2.13.

Огибающая пунктирная кривая представляет изменяющуюся амплитуду колебаний в волновом пакете, основная частота которых < w >. Энергия такого волнового пакета сосредоточена в сравнительно небольшом интервале частот. Поэтому волновые пакеты называются также импульсами. Мы будем использовать оба эти названия в зависимости от обстоятельств. Максимальная амплитуда образуется в точке t = 0, когда все колебания складываются в одинаковой фазе. Через промежуток времени t, определяемый условием

амплитуда колебаний обращается в нуль. Это время принимается за меру длительности центрального импульса. Поэтому между частотным интервалом слагаемых колебаний D w = 2 p D n и временной продолжительностью импульса существует соотношение

,

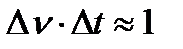где использован знак приблизительного равенства, что учитывает произвольность в определении продолжительности импульса. Такое соотношение уже было получено при анализе спектрального состава прямоугольного импульса. Ввиду универсальности соотношения его часто называют теоремой о ширине частотной полосы.

Date: 2015-08-06; view: 450; Нарушение авторских прав