Уравнение движения электропривода

Работа электропривода часто сопровождается изменени­ем скорости движения его звеньев, что вызывается рядом при­чин: колебаниями механической нагрузки, включением и вы­ключением пусковых и тормозных резисторов, изменениями напряжения питания, воздействиями со стороны системы управления и т. д. При этом привод ускоряется или замедля­ется, появляются инерционные (динамические) силы или мо­менты, которые двигатель должен преодолевать, находясь в переходном режиме. Таким образом, переходный режим – это режим работы при переходе от одного установившегося состояния к другому, когда изменяются скорость, момент, ток и др. Исследование характера движения рабочего органа про­изводится, как правило, на основе решения уравнения дви­жения. Уравнение движения электропривода должно учиты­вать все силы и моменты, действующие в установившихся и переходных режимах.

Согласно уравнению равновесия сил и моментов получим для поступательного и вращательного движения [2, 3, 4, 5]

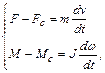(1.16)

где F_c и М_с, т и J – приведенные сила и момент сопротивления, масса и момент инерции; 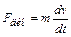, 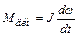– динамические (инерционные) составляющие силы и момента; F, М – сила, момент двигателя.

Сама электрическая машина (двигатель) в системе приво­да может работать в двигательном (знак «+») и тормозном (знак «-») режимах, поэтому (1.16) в более общем виде запишется

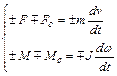(1.17)

Выбор знаков в (1.17) зависит от режима работы двигате­ля и характера моментов сопротивления. Из анализа (1.16, 1.17) видно, что при J = const:

1) М>М_с, 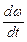=ε>0, имеет место разгон (ускорение) при­вода, электрическая энергия преобразуется в механическую;

2) если М<М_С, 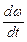<0, имеем замедление (торможение) привода;

3) при М = М_с, 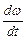= 0 привод работает в установившемся режиме.

Динамический момент проявляется только во время пере­ходных процессов, когда изменяется скорость привода (ана­логия: ЭДС самоиндукции e = L 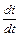будет только при измене­нии тока), он определяется алгебраической суммой моментов двигателя и сопротивления как по величине, так и по знаку.

Интегрированием уравнения (1.16) определяют время пе­реходных процессов при заданных возмущающих воздейст­виях (изменение 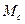, напряжения и др.).

Разделив переменные, получим

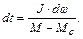(1.18)

Время изменения скорости от 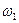до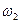

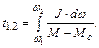(1.19)

Для решения этого уравне­ния необходимо знать механи­ческие характеристики двигате­ля и механизма, т. е. 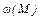и 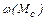. При допущении, что 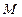= const, M_c = const, J = const

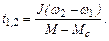(1.20)

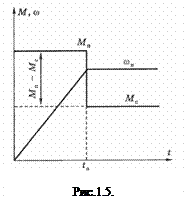
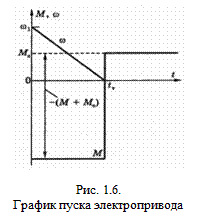
По этому выражению мож­но определить время пуска двигателя, приняв 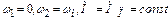(рис. 1.6).

Для пуска на холостом ходу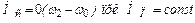

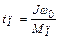(1.21)

При замедлении привода динамический момент имеет от­рицательное значение, т. е. -М - М_с = 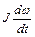, или же двига­тель развивает положительный момент, но по величине мень­ший момента сопротивления. В этом случае время торможения

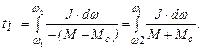(1.22)

В случае М = const, M_c = const получим (рис. 1.7)

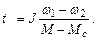(1.23)

Из рис. 1.6, 1.7 видно, что при принятых допущениях зависимости являются пря­мыми, наклон которых зависит от момента (М - М_с) или (М + М_с) и момента инерции.

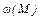Если и 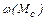явля­ются сложными функциями, то уравнение движения привода (1.17) аналитически не решает­ся. В таких случаях пользуются приближенными графическими или графоаналитическими ме­тодами решения [2, 3, 4, 5].

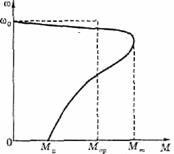
Пример. Оценить время разгона вхолостую асинхронно­го двигателя, имеющего харак­теристику 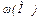, показанную на рис. 1.8. При этом: 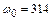рад/с, 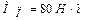, макси­мальный момент 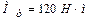, момент инерции ротора .

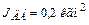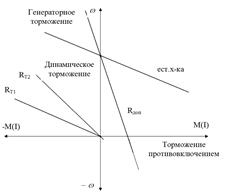
Рис. 1.7. График торможения электропривода

Точное определение времени пуска затруднено из-за не­линейной характеристики 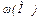. Если момент за время пуска усреднить, т. е. реальную характеристику заменить прямо­угольной, когда 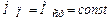, то получим из (1.20, 1.21):

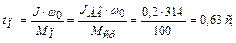
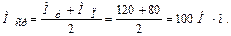
Очевидно, что минимум времени разгона имеет место при наибольшем ускорении. Пусть М_с = const, а КПД механиче­ской передачи (редуктора) равен единице, тогда (1.16) может быть записано в виде

, (1.24)

где 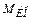– момент нагрузки исполнительного органа. Отсюда ускорение исполнительного органа

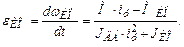(1.25)

Максимум ускорения будет при 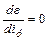. В итоге получим оптимальное значение передаточного отношения

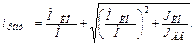(1.26)

Если 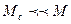, то (1.29) запишется в виде

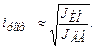(1.27)

Из (1.27) очевидно, что чем больше момент инерции про­изводственного механизма J_ио по сравнению с J_дв, тем выше должно быть передаточное число i_p редуктора. Вопрос выбора передаточного числа редуктора особенно важен в приводах, работающих в повторно-кратковременных режимах S3.

Date: 2015-08-06; view: 974; Нарушение авторских прав