Дербес туынды. Мысалдар

Егер 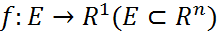функциясы а нүктесінде дифференциалданса онда

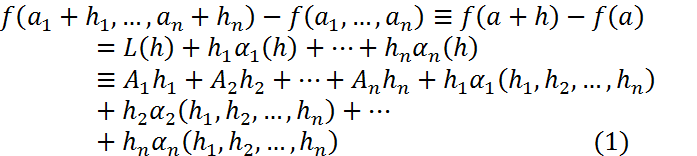
(1)aнықтамасындағы 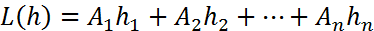сызықтыфункциясы f функциясының а нүктесіндегі дифференциалы деп аталады.

Әуелі n=2 болған жағдайда 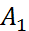-ди f арқылы белгілейік. Ол үшін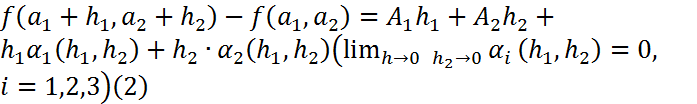

теңдігінде =0 деп алсақ, онда болады. Бұл теңдіктің екі жағын да 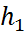-ге бөліп,

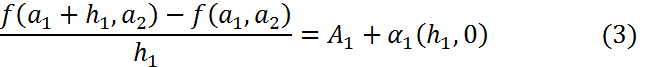теңдігін келеміз, ал 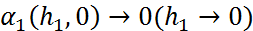болғандықтан, 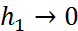болғанда (3)-дің оң жағындағы өрнектің шегі бар және ол тең, демек, (3) сол жағындағы өрнектің де шегі бар және ол да 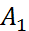-ге тең:

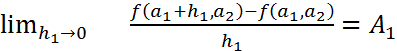(4)

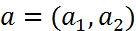нүктесі үшін 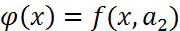f функциясының бірінші аргументін тәуелсіз айнымалы ретінде алып, екінші аргументін 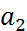–ге тең етіп алып, 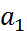нүктесінде 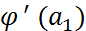туындысын есептесек, онда дәл 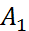-ге келеміз, өйткені

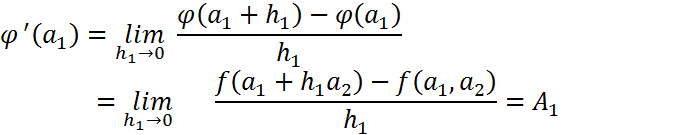
үшін де

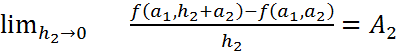теңдігі орындалатын дәл осылай дәлелденеді. Осыған сүйеніп, келесі маңызды анықтаманы енгізейік.

f(x) cандық функциясы 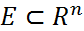ашық жиынында анықталып, 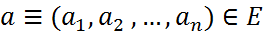болсын. Егер

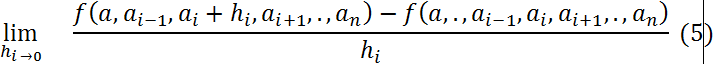
шегі бар және ол нақты сан болса, онда фукнциясының а нүктесіндегі і-ші айнымалы бойынша дербес туындысы бар дейді де (5) шегінің мәнін f фукнциясының і -ші айнымалы бойынша дербес туынды деп атап, 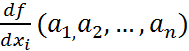(3) өренгін былайда түсінуге болады: 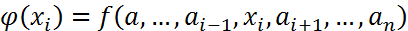бір айнымалылы функциясын қарастырып, осы 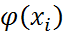функциясын 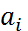нүктесінде арқылы туындысы бар болса, онда сол туынды f(x) функциясының а нүктесінде і -ші айнымалы бойынша алған дербес туындының дәл өзі болады.

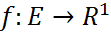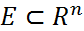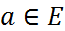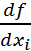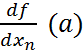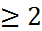1-теорема. функциясы ашық ж-да анықталып, болсын. Егер f ф–сы а нүктесінде дифф-са, онда (a),…, дербес туындылары бар болып, болады. Әрбір n үшін барлық айнымалылары бойынша дербес туындылары бар болатын нүктеде n айнымалылы функция дифф-бауы мүмкін.

2-теорема. Егер f ф-сы а нүктесінде дифф-са, онда ол сол нүктеде үзіліссіз де болады. Үзіліссіз ф-ия дифф-бауы мүмкін.

Мысалы,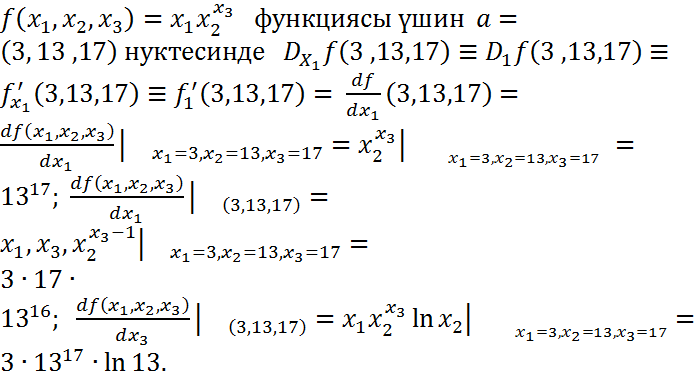

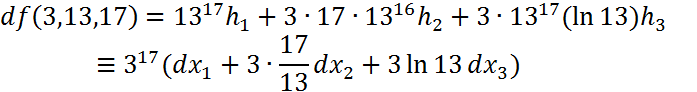
Date: 2015-07-24; view: 2831; Нарушение авторских прав