Учет влияния износа. Применение нормального закона распределения. Интеграл вероятности и нормальная функция распределения, их применение в расчетах надежности

Наиболее целесообразно использовать элементы в течение времени нормальной эксплуатации, так как в этот период интенсивность отказов принимает минимальное значение. Однако это не всегда возможно и экономически не целесообразно. Поэтому многие элементы работают в течение времени, когда начинает сказываться износ на 3 участке. Опыт показывает, что для 3-го участка распределение отказов элементов из-за износа подчиняется нормальному закону распределения: 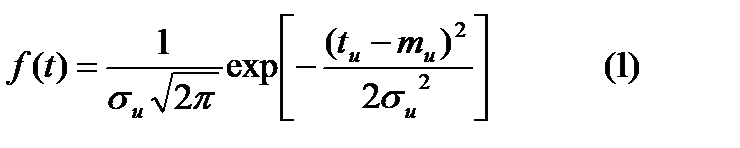, где -общее время эксплуатации, , - мат ожидание и среднее квадратическое отклонение. для данного типа элементов приближенно можно определить по формуле: 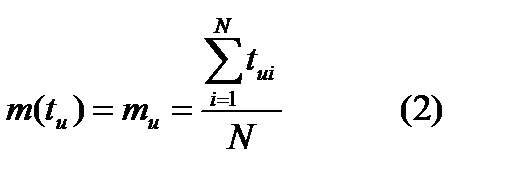, 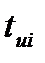-время работы до износового отказа i-го элемента, N-число элементов над которыми проводится испытание.

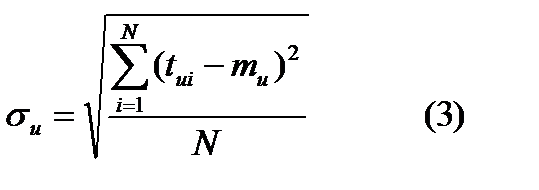. В реальных условиях определить очень трудно. 1)Для получения удовлетворительной точности необходимо большое число элементов. 2) Очень трудно определить причину отказа.

Предположим, что известны параметры нормального закона распределения, тогда интегрированием:

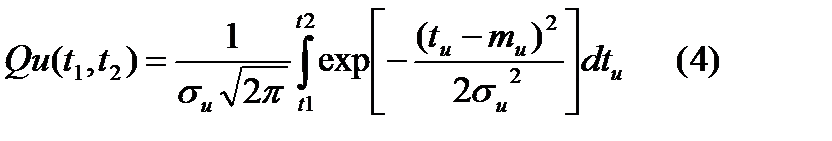. Вся площадь под кривой (t₁..t₂) – это вероятность численно равная длине отрезка В в функции Q(t).

Задача по определению вероятности отказа элементов в течении заданного интервала времени полностью аналогична задаче попаданию случайной величины, подчиненной нормальному закону в заданный отрезок.

Случайная величина –время износового отказа. Из теории вероятности известно, что эта задача решается с помощью интеграла вероятности Ф(х), где х – случайная величина. Величина Ф(х) может быть заменена на Ф*(х), где * - нормальный закон распределения. Функция распределения 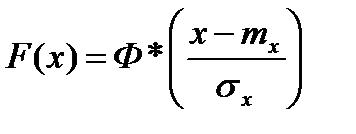, где параметры нормального закона распределения случайной величины х.

х=t, 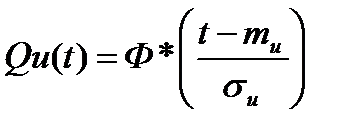, тогда вероятность отказа элемента в интервал t₁, t₂ : 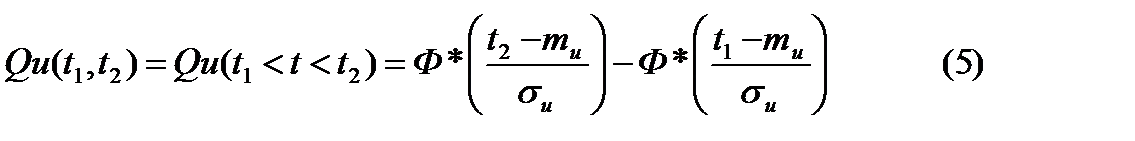. Вероятность безотказной работы в интервале времени t₁, t₂ (при условии, что в момент времени t₁-элемент работоспособен) будет определяться равенством: 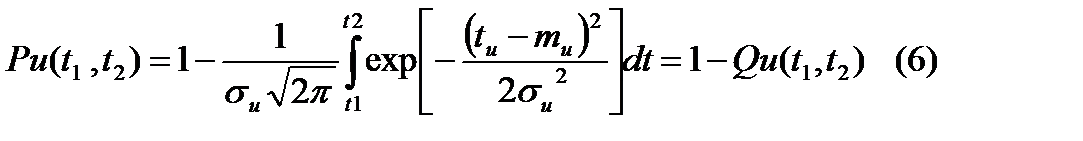. Если требуется определить вероятность безотказной работы элемента в течение времени от начала эксплуатации до момента времени t₃, то оно может быть найдено по формуле: 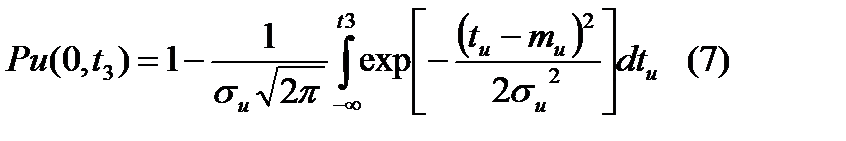, 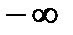не имеет физического смысла, так как элемент начинает работать в момент времени 0, однако вероятность безотказной работы в интервале 0, t₃ есть вероятность того, что отказ произойдет в течение интервала времени, лежащего правее точки t₃, потому (7) записывается в виде: , выражение (8) может быть найдена с помощью нормальной функции распределения, т.е. вероятностью безотказной работы:

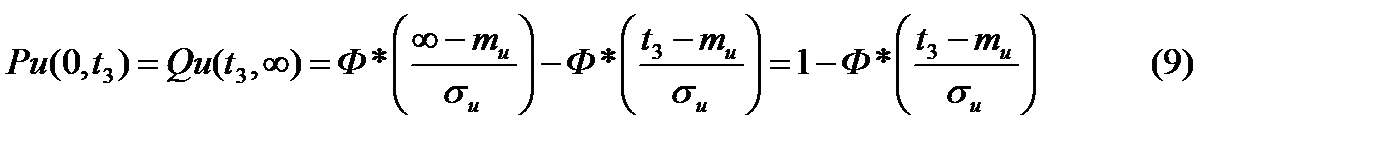. Для любого интервала времени (0,t) вероятность безотказной работы будет определяться по формуле: , . Возможны случаи когда требуется определить вероятность того, что элемент начавший работать в момент времени равный 0, будет безотказно работать в интервале времени t₁, t₂, если заранее неизвестно будет ли он работоспособен в момент времени t₁. Очевидно, что для этого необходимо чтобы элемент проработал безотказно в момент времени t₁, а далее t₁, t₂. По теории умножения вероятностей. Вероятность безотказной работы в течение времени t₁, t₂ равна условной вероятности того, что элемент проработает безотказно в течение времени t₁, t₂.

, подставляя в (12): , принимаем нормальную функцию распределения получаем:

.

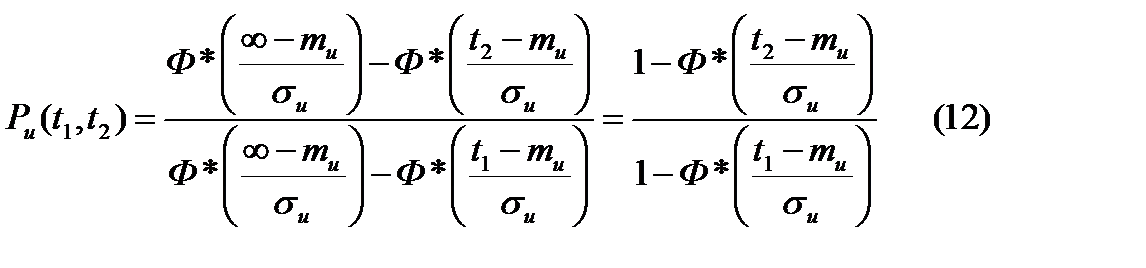Интенсивность износовых отказов определяется: 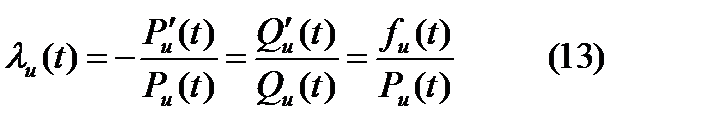. При нормальном законе распределения равенство (13) запишется в виде:

.

Date: 2015-07-23; view: 663; Нарушение авторских прав