Порождающая и проверочная матрицы

Порождающей матрицей линейного 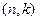-кода называется матрица размера 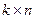, строки которой – его базисные векторы.

Например,

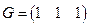
является порождающей матрицей кода из двух слов {000, 011}.

Матрица

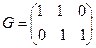
является порождающей для кода В из примера 6.3.

Мы знаем, что кодовые слова – линейные комбинации базисных векторов, т.е. строк матрицы 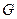. Это означает, что слова могут быть получены умножением вектора на матрицу. Итак, сообщение записывается в виде вектора 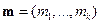и соответствующее сообщению кодовое слово вычисляется по формуле

.

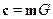Тем самым вектор из бит превращается в последовательность из 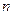двоичных символов, передаваемых по каналу или записываемых в память запоминающего устройства.

Обратимся к задаче декодирования.

Предположим, что для некоторого двоичного вектора 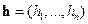все кодовые слов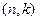а -кода 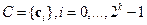, удовлетворяют тождеству

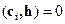, , (6.2)

в котором 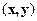обозначает скалярное произведение векторов 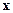и .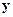

Про такой вектор 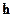мы скажем, что он ортогонален. Найдя такой вектор, мы могли бы проверять с помощью тождества (6.2), является ли принятая из канала последовательность кодовым словом.

Заметим, что (6.2) справедливо для всех кодовых слов, если оно справедливо для базисных векторов, т.е. если

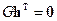, (6.3)

где верхний индекс Т обозначает транспонирование.

Чем больше таких «проверок» мы найдем, тем, по-видимому, больше ошибок сумеем обнаружить и исправить.

Упражнение 6.4. Докажите, что проверки образуют линейное пространство.

Это пространство назовем пространством, ортогональным линейному коду или проверочным пространством.

Упражнение 6.5. Найдите размерность линейного пространства проверок.

Чтобы выполнить последнее упражнение, нужно заметить, что в матрице 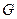имеется ровно линейно независимых столбцов. Не больше (почему?) и не меньше (почему?). Зафиксируем список номеров этих столбцов и назовем этот набор чисел информационной совокупностью. Чуть позже смысл этого названия станет яснее. Выберем произвольно значения вектора 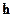на позициях, не входящих в информационную совокупность. Какими должны быть значения на позициях информационной совокупности, чтобы выполнилось (6.3)? Чтобы ответить на этот вопрос, придется решить систему линейных уравнений, причем система имеет единственное решение.

Следствием этих рассуждений является теорема

Теорема. Размерность проверочного пространства линейного 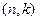-кода равна .

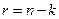Базис проверочного пространства запишем в виде матрицы

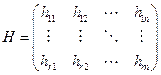
называемой проверочной матрицей кода.

Проверочная и порождающая матрицы связаны соотношением

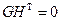. (6.4)

Из этого соотношения мы видим, что для любого кодового слова 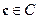имеет место

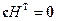. (6.5)

Это тождество можно использовать как критерий принадлежности произвольной последовательности коду, т.е. для обнаружения ошибок.

Зная, 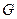можно найти 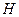. Для того, чтобы понять, как это сделать, заметим, что один тот же код можно задать разными порождающими матрицами, выбирая по-разному базис пространства. Больше того, заменив в 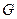любую строку на любую линейную комбинацию этой строки с другими строками, мы получаем новую порождающую матрицу того же кода.

Перестановка столбцов матрицы 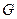, вообще говоря, приводит к другому коду, но этот другой код по своим характеристикам не отличается от исходного. Коды, различающиеся только нумерацией позиций, называются эквивалентными.

Понятно, что для каждого кода найдется эквивалентный, для которого первые позиций образуют информационную совокупность, т.е. первые столбцов образуют невырожденную матрицу размера 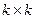. Заменяя строки линейными комбинациями строк (метод Гаусса) полученную матрицу можно привести к виду

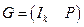, (6.6)

где 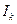– единичная матрица порядка , а 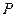– некоторая матрица размера .

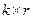Матрица вида (6.6) называется порождающей матрицей, приведенной к систематическому виду, а соответствующий код называется систематическим. Кодирование для систематического кода немного проще, чем для кода общего вида:

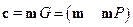, (6.7)

т.е. в кодовом слове первые позиций – просто копия информационной последовательности 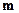, а остальные 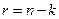(проверочных) позиций получаются умножением информационного вектора на матрицу размера 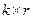, что иногда существенно меньше, чем 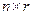. Соответственно, и информация о систематическом коде занимает существенно меньше памяти, чем информация о линейном коде общего вида.

Для систематического кода с порождающей матрицей в форме (6.6) проверочная матрица может быть вычислена по формуле

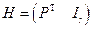. (6.8)

Упражнение 6.6. Проверьте (6.7). Подсказка: для этого нужно подставить (6.8) и (6.6) в (6.4).

Как найти проверочную матрицу для несистематического кода?

Очень просто. Нужно привести матрицу к систематическому виду и воспользоваться (6.7). Если первые столбцов порождающей матрицы образуют невырожденную подматрицу (первые позиций образуют информационную совокупность), то для приведения к систематической форме достаточно таких операций как перестановка строк и замена строк линейными комбинациями строк. Если нет – нужно будет сначала найти информационную совокупность и перенумеровать позиции так, чтобы первые позиции стали информационными.

Упражнение 6.7. Сформулируйте алгоритм нахождения порождающей матрицы по проверочной.

Упражнение 6.8. Объясните, почему любой набор номеров линейно-независимых столбцов называется информационной совокупностью.

Упражнение 6.9. Постройте порождающие и проверочные матрицы для кодов из примера 6.4.

Подведем итоги этого важного параграфа.

Линейный 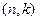-код может быть задан любой из двух матриц: порождающей 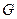размера 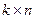либо проверочной 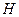размера 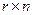. По 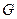легко найти 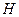приведением кода к систематической форме. Аналогично по 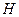находится .

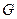Матрица 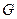используется при кодировании (формула (6.7)), матрицей 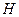можно воспользоваться при декодировании. Например, выполнение тождества (6.5) свидетельствует о том, что данная последовательность принадлежит коду.

Date: 2015-07-10; view: 6899; Нарушение авторских прав