Примеры кодов

Сформулированные в упражнениях свойства линейных кодов позволяют построить коды с маленькими расстояниями.

Пример 6.4. Код с порождающей матрицей

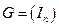
представляет собой 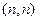-код со скорость 1 и минимальным расстоянием 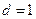. Поскольку число проверочных символов 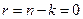, проверочная матрица неопределена. Заметим, что код удовлетворяет границе Синглтона.

Пример 6.5. Из упражнения 6.10 понятно, что 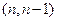-код с проверочной матрицей

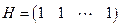
(вектор из 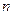единиц) имеет минимальное расстояние 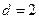. Его порождающая матрица имеет вид

.

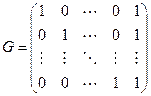Этот код – самый экономный код, позволяющий ценой одного избыточного символа обнаруживать любые однократные ошибки и любые другие комбинации ошибок нечетного веса. Его называют кодом с проверкой на четность.

Отметим, что и этот код удовлетворяет границе Синглтона.

Пример 6.6. Пусть

.

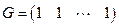Этот код – двойственный к коду предыдущего примера. Очевидно, в таком коде всего два слова, т.е. имеем 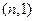-код. Его проверочная матрица

.

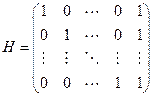Расстояние кода 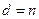, он исправляет до половины ошибок при передаче кодового слова.

Пример 6.7. Построим код, исправляющий любые однократные ошибки. Для этого нужно составить проверочную матрицу из различных столбцов (см. упражнение 6.11). При числе проверочных символов 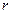длина кода равна 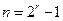, а число информационных символов равно 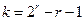. Такие 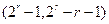-коды называются кодами Хэмминга. Таким образом, имеем бесконечную последовательность кодов с расстоянием 3.

В качестве примера рассмотрим случай 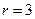, т.е.

.

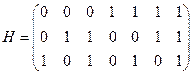Очевидно, столбцы с номерами 5, 6 и 7 линейно независимы. Используя этот факт, находим порождающую матрицу

.

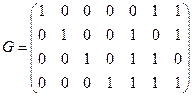Для кода Хэмминга легко указать процедуру исправления ошибок. Предположим, что передаваемое сообщение имеет вид 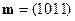. Ему соответствует кодовое слово .

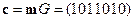Предположим, что при передаче этой последовательности произошла ошибка и принятая последовательность имеет вид

,

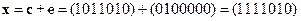где через 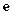обозначен вектор ошибки.

Декодер начинает с проверки того, является ли принятая последовательность кодовым словом. По формуле (6.5) находим

.

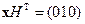Полученная последовательность оказалась двоичной записью номера ошибочной позиции. Легко убедиться в том, что это верно для любой одиночной ошибки. Попробуйте объяснить, почему это свойство имеет место.

Упражнение 6.15. Получите из кода Хэмминга кода с минимальным расстоянием .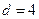

На этом мы заканчиваем рассмотрение кодов, исправляющих ошибки.

Смысл нашего короткого введения – демонстрация одного из изящных и далеко не тривиальных способов внесения избыточности в передаваемую информацию с целью повышения надежности ее передачи либо хранения.

Date: 2015-07-10; view: 936; Нарушение авторских прав