Система с резервированием и восстановлением

Рассмотрим теперь пример задачи, в которой нам придется иметь дело с марковским процессом непрерывного времени. По аналогии с процессами дискретного времени, процесс считается Марковским, если при известном состоянии процесса в некоторый момент времени 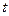, распределение вероятностей на множестве состояний в последующие моменты времени не зависит от состояний процесса в моменты времени, предшествующие .

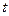Предположим, что система содержит некоторое число 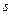идентичных устройств, которые поочередно включаются в работу по мере выхода других устройств из строя. Модель отказов устройств считаем экспоненциальной с интенсивностью 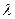, а модель процесса восстановления каждого устройства – экспоненциальной с параметров 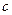. Подсчитаем вероятность того, что в некоторый момент времени 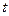все устройства будут неисправны. Эта вероятность представляет собой коэффициент простоя системы.

Подобная задача решается в теории систем массового обслуживания. Вместо потока отказов рассматривается поток заявок на обслуживание, а роль процессов восстановления играют процессы обслуживания заявок. Подсчитывается вероятность отказа в обслуживании – вероятность того, что в некоторый момент времени все 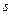обслуживающих устройств заняты.

Чтобы вычислить искомую вероятность, найдем стационарное распределение вероятностей на множестве состояний рассматриваемой цепи Маркова. Для этого обозначим через 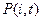распределение вероятностей на множестве состояний 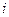(на множестве значений 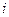числа неисправных устройств) в момент времени 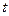. Задача состоит в вычислении стационарных вероятностей

.

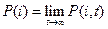Искомая вероятность – это вероятность .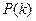

Рассмотрим моменты времен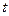и и 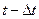, разделенные малым промежутком 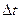. По формуле полной вероятности можно записать

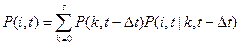, (3.24)

где роль гипотез играет число неисправных устройств в момент 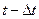. Остановимся на вычислении условной вероятности 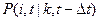, которая представляет собой вероятность перехода из состояния в состояние 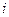за время 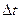. Введем обозначение 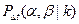для вероятности того, что за время 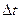произойдет 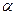отказов и 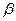восстановлений при наличии неисправных устройств. Имеем

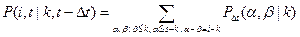, (3.25)

где суммирование выполняется по таким парам 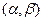, для которых выполнены условия: 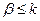(число восстановленных устройств не может быть больше числа неисправных устройств), 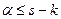(число отказавших устройств не больше числа исправных устройств), и очевидное условие 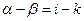необходимое для перехода системы из состояния в состояние .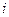

В силу независимости процессов отказов и восстановлений

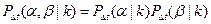. (3.26)

Поскольку процессы отказов и восстановлений – простейшие, вероятности значений 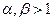имеют более высокий порядок малости по сравнению с вероятностями значения 1. Получаем

,

,

,

,

,

,

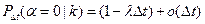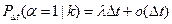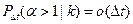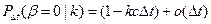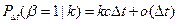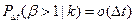Здесь, в частности, мы приняли во внимание, что

.

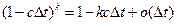Подстановка полученных соотношений в (3.26) дает

,

,

,

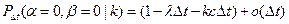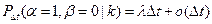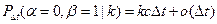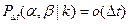при .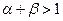

Последующая подстановка результата в (3.25) приводит к соотношениям

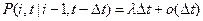
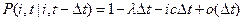
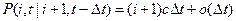
Эти условные вероятности мы должны подставить в (3.24). Чтобы сократить запись, сразу перейдем к пределу при 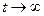и поэтому заменим слева и справа вероятност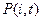и и 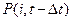на их стационарные значения 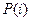. Кроме того, заметим, что слагаемое 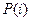присутствует справа и слева, поэтому сокращается, а все остальные слагаемые можно поделить на 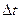. Переходя к пределу при 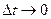приходим к разностному уравнению

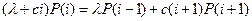, (3.27)

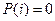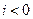на решение которого накладывается ограничения при и 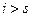, и условие нормировки вероятностей

.

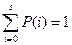При 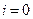имеем

, .

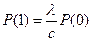При 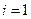имеем

, .

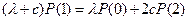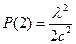Продолжая, приходим к общей формуле

.

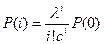Из условия нормировки выводим окончательную формулу

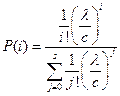, (3.28)

которую в теории массового обслуживания называют первой формулой Эрланга.

Заметим, что при 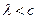(если интенсивность отказов меньше интенсивности восстановлений) вероятность 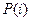убывает с увеличением 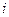. При этом коэффициент простоя 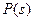будет быстро убывать с увеличением числа доступных устройств 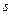. Если же 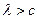, то вероятность 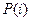возрастает с увеличением 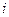и коэффициент простоя будет большим при любом числе устройств.

Date: 2015-07-10; view: 569; Нарушение авторских прав