Арифметика пространства двоичных последовательностей

Над двоичными символами можно выполнять операции сложения и умножения. Мы рассматриваем числа 0 и 1 как элементы кольца вычетов по модулю 2 и как группу по умножению. Иными словами, множество чисел {0,1} образует простейшее поле из двух элементов 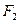. Таблицы сложения и умножения показаны на рис. 6.1.

Рис. 6.1. Таблицы сложения и умножения в поле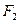

От вычисления над скалярными элементами можно перейти к изучению действий над последовательностями (векторами). Для произвольного множества 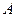мы через 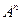обозначаем множество последовательностей длины 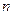, составленных из элементов множества .

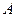Определим сумму векторов 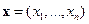и 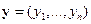как покомпонентную сумму 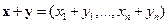. Умножение вектора 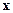на скалярную величину 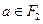определим как .

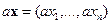Множество векторов, замкнутое относительно операций сложения и умножения на скаляр, называется линейным векторным пространством.

Пример 6.3. Примеры двоичных линейных пространств:

А)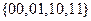

Б)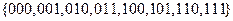

В) . ■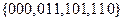

Множество 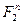всех двоичных последовательностей длины 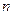, очевидно, является линейным пространством. Так, пространства А и Б совпадают с 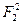и 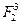. Такие пространства содержат в общем случае 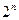векторов. Пространство В содержится в 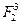но не совпадает с ним, т.е. является его линейным подпространством.

Заметим, что каждое из трех пространств примера 6.3 содержит нулевой вектор. Этим свойством обладает любое линейное пространство (почему?).

Ключевым понятием в описании линейных пространств является понятие базиса.

Базисом линейного пространства называется наибольшее возможное множество линейно независимых векторов пространства. Число базисных векторов называется размерностью пространства.

Пример 6.4. Для линейных пространств примера 6.3 имеем:

А) Размерность равна 2, пример базиса: {01,10}

Б) Размерность равна 3. Примеры базисов: {001, 010, 100}, {110, 011, 111}.

В) Размерность равна 2, пример базиса: {011, 101}. ■

Основное свойство базиса:

Любой вектор пространства единственным образом может быть представлен в виде линейной комбинации базисных векторов.

Доказательство: от противного. Оставляем читателю в качестве упражнения.

Наконец, все готово, о вперед, дадим определение линейного кода.

Линейным двоичным кодом 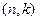-кодом 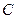называется любой -мерное подпространство пространства 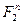всевозможных векторов длины .

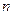Скоростью кода называется отношение 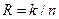(бит/символ).

Мы уже замечали, что хорошим будет код, слова которого «далеки» друг от друга в смысле расстояния Хэмминга

,

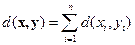где

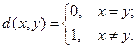
Расстояние Хэмминга удовлетворяет аксиомам расстояния:

1)

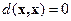
2) 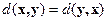(симметричность)

3) 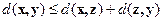(неравенство треугольника)

(проверьте это самостоятельно).

Таким образом, имеем метрическое пространство.

Минимальным расстоянием кода 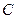называется наименьшее из попарных расстояний между кодовыми словами:

.

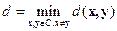Для линейного кода эта формула может быть упрощена:

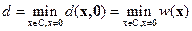, (6.1)

где 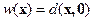- число ненулевых элементов в последовательности 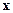или вес вектор в метрике Хэмминга.

Упражнение 6.1. Докажите (6.1).

Упражнение 6.2. Докажите, что код с минимальным расстоянием 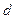исправляет любые комбинации ошибок кратности не больше .

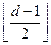Упражнение 6.3. Докажите, что код с минимальным расстоянием 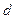обнаруживает любые комбинации ошибок кратности не больше .

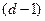После введения понятия базиса стало понятнее, как можно сэкономить память для хранения информации о коде: достаточно помнить не все пространство, а только его базис, а конкретные кодовые слова порождать в процессе кодирования. Это означает, что для (1000,500)-кода вместо 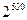кодовых слов достаточно хранить 500 базисных слов длины 1000. Для этого достаточно 500 кбит памяти. Таким объемом памяти никого сегодня не удивишь. На самом деле, и эта цифра завышена. Например, можно использовать циклические коды, в которых слова являются циклическим сдвигом друг друга. По сути, можно хранить только одно слово, т.е. всего 1000 бит. И даже это больше того, что требуется на практике.

В следующем параграфе мы сделаем первые шаги в направлении кодирования и декодирования двоичных данных.

Date: 2015-07-10; view: 1046; Нарушение авторских прав