Дискретные цепи Маркова

Анализ надежности систем методами теории цепей Маркова

Рассмотрим некоторую систему, состоящую из нескольких устройств, совместно решающих какую-то задачу. Это может быть, например, сеть связи, компьютерная сеть, многопроцессорное вычислительное устройство и т.п. При выходе из строя одного или нескольких устройств вся система может сохранять работоспособность, но ее надежность, конечно, снижается. Количество работающих устройств можно назвать состоянием системы и изучать последовательность состояний. Модель последовательности состояний несет информацию о надежности системы в целом.

Последовательность состояний системы представляет собой случайный процесс дискретного либо непрерывного времени. Разумеется, значения процесса в последовательные моменты времени зависимы и характер зависимости чрезвычайно важен. Процессы с зависимыми значениями называют еще процессами с памятью. Среди различных классов процессов с памятью особое место занимают цепи Маркова, которые и являются объектом рассмотрения в данной главе.

Дискретные цепи Маркова

Случайный процесс 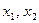,… со значениями 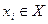, 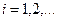задан, если для любых 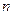указан способ вычисления совместных распределений вероятностей .

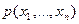Проще всего задать случайный процесс, предположив, что его значения в различные моменты времени независимы и одинаково распределены. Тогда

,

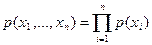где 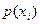– вероятность появления 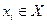в момент времени 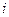. Для описания такого процесса достаточно указать вероятности 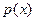для всех 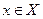(всего 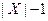вероятностей).

Описание более сложных моделей процессов будет громоздким, если не сделать упрощающих предположений. Нам не обойтись без предположения о стационарности.

Процесс называется стационарным, если для любых 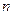и имеет место равенство

,

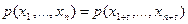в котором подразумевается, что , .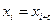

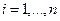Иными словами, случайный процесс стационарен, если вероятность любой последовательности не изменяется при ее сдвиге во времени (не зависит от положения последовательности на оси времени).

Числовые характеристики, в частности, математическое ожидание стационарных процессов не зависят времени. Рассматривая стационарные процессы, мы сможем вычислять независящие от времени информационные характеристики случайных процессов.

Простейшей моделью источника, порождающего зависимые сообщения, является марковский источник.

Случайный процесс 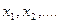называют цепью Маркова связности 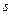, если для любых 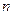и для любых 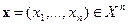справедливы соотношения

.

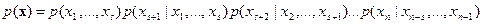Иными словами, мы называем марковским процессом связности 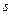такой процесс, для которого при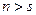

,

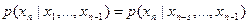то есть условная вероятность текущего значения при известных 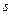предшествующих не зависит от всех других предшествующих значений.

Описание марковского процесса задается начальным распределением вероятностей на последовательностях из первых 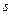значений и условными вероятностями вида 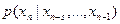для всевозможных последовательностей 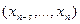. Если указанные условные вероятности не изменяются при сдвиге последовательностей 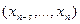во времени, марковская цепь называется однородной.

Однородная марковская цепь связности 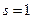называется простой цепью Маркова. Для описания простой цепи Маркова с множеством состояний 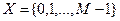достаточно указать начальное распределение вероятностей 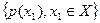и условные вероятности

, ,

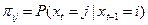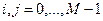называемые переходными вероятностями цепи Маркова.

Переходные вероятности удобно записывать в виде квадратной матрицы размерности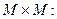

P ,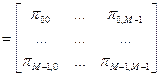

называемой матрицей переходных вероятностей. Эта матрица – стохастическая (неотрицательная, сумма элементов каждой строки равна 1).

Обозначим через 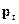стохастический вектор, компоненты которого – вероятности состояний цепи Маркова в момент времени 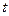, то есть 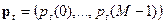, где 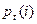есть вероятность состояния 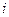в момент времени , 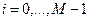. Из формулы полной вероятности следует, что

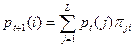
или в матричной форме

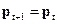P. (3.1)

Отсюда для произвольного числа шагов 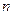получаем

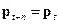P .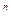

Значит, вероятности перехода за 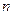шагов могут быть вычислены как элементы матрицы P .

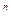Из (3.1) видим, что распределение вероятностей в момент времени зависит от величины и от начального распределения 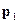. Отсюда следует, что в общем случае рассматриваемый случайный процесс нестационарен. Предположим, однако, что существует стохастический вектор 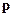, удовлетворяющий уравнению

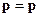P. (3.2)

Положим 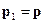. Тогда, воспользовавшись (3.1), получим 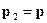и, в конечном итоге, 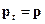при всех . Таким образом, однородная марковская цепь стационарна, если в качестве начального распределения выбрано решение уравнения (3.2).

Стохастический вектор 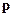, удовлетворяющий уравнению (3.2), называется стационарным распределением для цепи Маркова, задаваемой матрицей переходных вероятностей P.

Финальным распределением вероятностей называют вектор

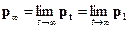P 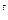, (3.3)

(если предел существует).

Из этого определения следует, что финальное распределение – распределение вероятностей в момент времени бесконечно далекий от начального момента времени 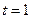. Было бы естественно ожидать, что оно не зависит от начального распределения 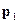. Оно не зависит также и от времени. Таким образом, распределение 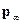тоже (как и 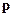), в некотором смысле, – стационарное распределение. Как же соотносятся между собо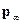й и ?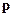

Оказывается, для широкого класса простых цепей Маркова предел в (3.3) не зависит от начального распределения 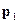и равен единственному решению уравнения (3.2), то есть 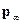= 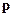. Такие цепи называют эргодическими.

Как определить по матрице P эргодична ли соответствующая цепь Маркова? Ответ заведомо положительный, если все элементы матрицы P положительны (не равны нулю). Более точное (но и сложнее проверяемое) условие состоит в том, что должна существовать некоторая положительная степень матрицы P такая, что все элементы матрицы P 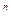положительны при любых .

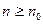Чтобы сформулировать необходимое и достаточное условие эргодичности, придется ввести еще несколько определений.

Состояние цепи 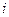достижимо из состояния 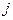, если для некоторого 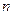вероятность перехода из состояния 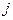в состояние 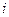за 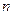шагов положительна. Множество состояний 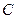называется замкнутым, если никакое состояние вне 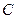не может быть достигнуто из состояния, входящего в .

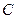Цепь называется неприводимой, если в ней не, больше одного замкнутого множества. Цепь Маркова неприводима, в частности, тогда, когда все ее состояния достижимы друг из друга.

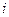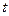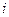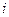Состояние называется периодическим, если существует такое >1, что вероятность перехода из в за 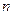шагов равна нулю при всех 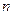не кратных 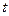. Цепь, не содержащая периодических состояний, называется непериодической.

Непериодическая неприводимая цепь Маркова эргодична.

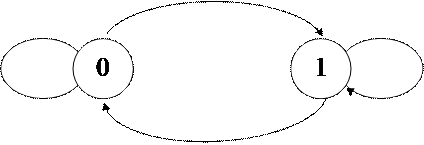
Пример 3.1. Двоичная цепь Маркова.

Date: 2015-07-10; view: 1610; Нарушение авторских прав