Расчет показателей надежности систем по показателям надежности отдельных элементов

Исходя из здравого смысла, всегда можно проанализировать множество ситуаций в работе системы или устройства, вычленить наиболее важные элементы, определяющие работоспособность системы в целом, и предложить некоторую математическую модель, описывающую работу системы. По этой модели можно пытаться аналитически или с помощью моделирования установить зависимости характеристик системы от характеристик ее элементов.

Приводимые ниже типовые структуры можно рассматривать как примеры «примитивов», которые можно использовать в качестве звеньев более сложных структур.

1. Последовательная структура, в которой отказ любого элемента ведет к отказу системы в целом. Ее можно условно представить в виде графа, показанного на рис. 4.1.

Обозначим через 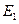, 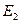и 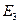булевы переменные, значения 1 которых соответствуют работоспособным состояниям устройств. Событие 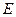описывает состояние системы в целом. Очевидно,

.

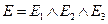Вероятность события 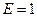(система исправна) выражается через вероятност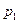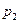и , и 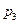исправной работы отдельных устройств формулой

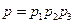. (4.1)

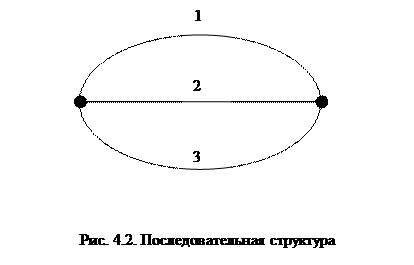
2. Параллельная структура, в которой для исправной работы системы достаточно, чтобы одно из устройств было исправно. Ей соответствует граф, показанный на рис. 4.2.

Формулы, связывающие работоспособность системы с работоспособностью ее частей, и соответствующая вероятность исправной работы системы имеют вид

;

=

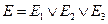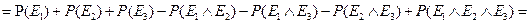
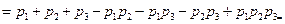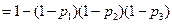. (4.2)

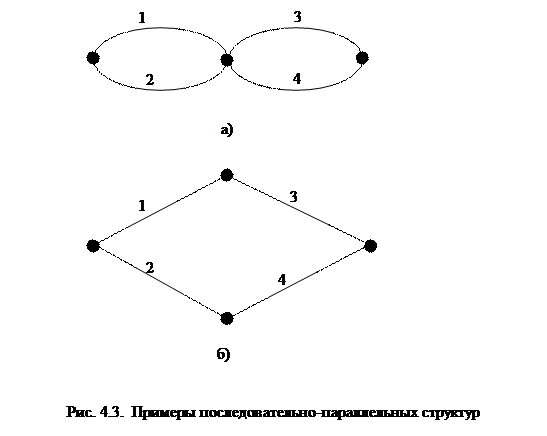
3. Последовательно-параллельные структуры. Читателю в качестве упражнения предлагается самостоятельно проанализировать схемы, показанные на рис. 4.3.

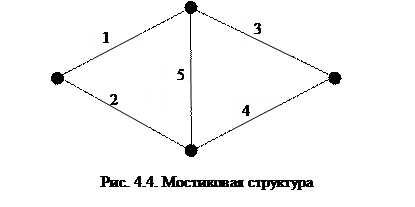
4. Мостиковая структура, показанная на рис. 4.4. Для этой схемы справедливы соотношения

.

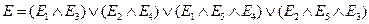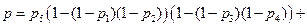
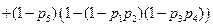. (4.3)

Последняя формула получена с помощью формулы полной вероятностей, при этом рассматриваются две гипотезы: элемент с номером 5 исправен и неисправен. В одном случае структура превращается в последовательно параллельную структуру, показанную на рис. 4.3а, во втором – в ту, что приведена на рис. 4.3б.

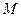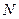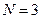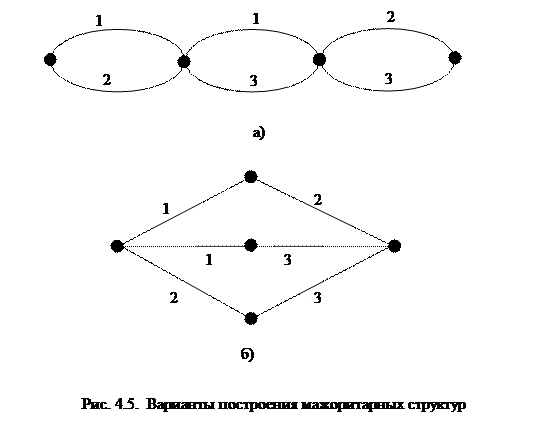
5. Мажоритарная структура. В общем виде имеется в виду, что, если исправно некоторое число из общего числа элементов, то и система в целом исправна. Примеры графов для случая , , 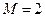показаны на рис. 4.5. Этой системе соответствует булева функция

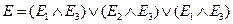
и вероятность работоспособного состояния равная

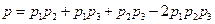. (4.4)

При записи формул вероятности успешной работы структур всякий раз предполагалась совместная статистическая независимость отказов устройств. Конечно, это предположение не всегда оправдано, поскольку отказы одних элементов могут влиять на работу других, например, менять режимы их работы. Кроме того, отказы элементов могут быть вызваны изменениями внешних условий, следовательно, условная вероятность отказа элемента будет различной при работоспособном и неработоспособном состоянии других элементов. Однако построить такую модель системы, в которой фигурировали бы условные вероятности отказов устройств, практически нереально.

Приведенные в данном параграфе формулы позволяют вычислить вероятность исправной работы системы в течение заданного интервала длительности 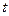, если такая информация известна для всех элементов системы. Меняя положение и длительность интервала 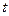, можно получить полное вероятностное описание системы и вычислить все ее характеристики надежности, рассмотренные в разделе 1.

Date: 2015-07-10; view: 598; Нарушение авторских прав