Вычисление минимального расстояния по проверочной матрице

Формула (6.1) нахождения минимального расстояния в терминах порождающей матрицы записывается как

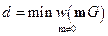. (6.8)

Вычисление по этой формуле требует перебора по 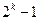ненулевым словам кода. Возвращаясь к примеру (1000,500)-кода, легко понять, почему на практике мы часто пользуемся кодами, минимальное расстояние которых никому не известно.

В тех случаях, когда 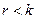, т.е. скорость кода больше 1/2, проверочная матрица имеет меньший размер, чем порождающая. Нельзя ли воспользоваться этим для упрощения поиска минимального расстояния кода?

Согласно формуле (6.5) кодовому слову 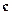веса 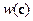соответствует некоторый набор 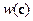столбцов, сумма которых – нулевой вектор. Это означает, что соответствующие столбцы линейно зависимы. Следовательно, для нахождения минимального расстояния кода нужно найти минимальный набор линейно зависимых столбцов. Приходим к следующей теореме.

Теорема. Минимальное расстояние линейного 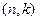-кода равно 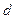в том и только в том случае, когда любые 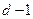столбцов линейно независимы и существует набор из 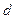линейно зависимых столбцов.

Подумав над тем, сколько всего может быть линейно независимых столбцов в матрице с 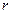строками, получаем следующую интересную границу на минимальное расстояние.

Теорема 6.3. ( Граница Синглтона ) Минимальное расстояние линейного 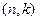-кода удовлетворяет неравенству .

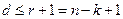Упражнение 6.10. Докажите, что если в 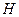нет нулевых столбцов, то минимальное расстояние кода не меньше 2.

Упражнение 6.11. Докажите, что если в 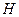все столбцы различны, то минимальное расстояние кода не меньше 3.

Упражнение 6.12. Докажите, что если одна из строк 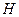не содержит нулей, то минимальное расстояние кода четно.

Упражнение 6.13. Найдите минимальные расстояния кодов примера 6.3.

Дуальным к данному коду называется код, порождающая матрица которого совпадает с проверочной матрицей данного кода.

Упражнение 6.14. Найдите минимальные расстояния кодов дуальных к кодам примера 6.3.

Date: 2015-07-10; view: 1955; Нарушение авторских прав