
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ГЛАВА 7. Подобные треугольники
|
|
Подобные треугольники
§ 1. Определение подобных треугольников.
56.
○ Определение. Отношением отрезков АВ и СD называется отношение их длин.
○ Определение. Отрезки АВ и CD называются пропорциональными отрезкам A 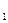 B
B 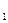 и C
и C 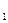 D
D 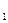 , если
, если 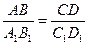 .
.
57.
○ Определение. Если все углы одного треугольника соответственно равны углам другого треугольника, то сходственными сторонами называются стороны этих треугольников, лежащие против соответственно равных углов.
n Определение. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
○ Определение. Коэффициентом подобия называется число, равное отношению сходственных сторон подобных треугольников.
58.
n Теорема (об отношении площадей подобных треугольников). Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
○ Теорема (Свойство биссектрисы треугольника (N 535)). Биссектриса треугольника делит противоположную сторону треугольника на отрезки, пропорциональные прилежащим сторонам треугольника.
§ 2. Признаки подобия треугольников.
59.
● Теорема (1 признак подобия треугольников). Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
60.
n Теорема (2 признак подобия треугольников). Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
61.
● Теорема (3 признак подобия треугольников). Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
○ Теорема (Фалеса, расширенная (N 556)). Если стороны угла пересечены параллельными прямыми, то отрезки, отсекаемые ими на одной его стороне, пропорциональны отрезкам, отсекаемым на другой его стороне.
§ 3. Применение подобия к доказательству теорем и решению задач.
62.
Определение. Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
● Теорема (Свойство средней линии треугольника). Средняя линия треугольника параллельна одной из его сторон и равна ее половине.
○ Теорема (Свойство медиан треугольника). Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.
63.
○ Теорема. Высота прямоугольного треугольника, проведенная к гипотенузе, разделяет треугольник на два подобных треугольника, каждый из которых подобен данному треугольнику.
○ Определение. Средним пропорциональным между отрезками AB и CD (или средним геометрическим) называется отрезок XY, если 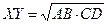 .
.
○ Замечание 1 (свойство высоты прямоугольного треугольника). Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между отрезками, на которые она делит гипотенузу.
○ Замечание 2. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между этим катетом и высотой, проведенной к гипотенузе.
§ 4. Соотношения между сторонами и углами прямоугольного треугольника.
66.
Определение. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Определение. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Определение. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
○ Определение. Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
○ Замечание 1. Тангенс угла равен отношению синуса этого угла к косинусу.
○ Замечание 2. Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы, косинусы и тангенсы этих углов равны соответственно.
Теорема (основное тригонометрическое тождество). 
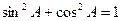 .
.
ГЛАВА 8
Окружность
§ 1. Касательная к окружности.
68.
* ○ Теорема 1. Если расстояние от центра окружности до прямой меньше ее радиуса, то прямая и окружность имеют ровно 2 общие точки.
* ○ Теорема 2. Если расстояние от центра окружности до прямой равно ее радиуса, то прямая и окружность имеют ровно 1 общую точку.
* ○ Теорема 3. Если расстояние от центра окружности до прямой больше ее радиуса, то прямая и окружность не имеют общих точек.
○ Определение. Секущей по отношению к окружности называется прямая, которая имеет с ней 2 общие точки.
69.
* ○ Определение. Касательной к окружности называется прямая, имеющая с ней только одну общую точку.
n Теорема (Ссвойство касательной). Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
● Теорема. Отрезки касательных, проведенные из одной точки к одной окружности, равны.
● Теорема. Отрезки касательных, проведенные из одной точки к одной окружности, составляют равные углы с прямой, проходящей через эту точку и центр окружности.
* ● Теорема (Признак касательной). Если прямая перпендикулярна радиусу и проходит через его конец, лежащий на окружности, то она – касательная.
§ 2. Центральные и вписанные углы.
70.
○ Определение. Дугой окружности называется каждая из двух частей, на которые две точки разделяют окружность.
○ Определение. Полуокружностью называется дуга, концы которой соединяет диаметр этой окружности.
* ○ Определение. Центральным углом окружности называется угол с вершиной в центре окружности (а стороны ее пересекают).
○ Определение. Градусная мера дуги, которая меньше полуокружности (или равна), считается равной градусной мере центрального угла, стороны которого проходят через ее концы.
○ Определение. Градусная мера дуги, которая больше полуокружности, считается равной 360° без градусной меры центрального угла, стороны которого проходят через ее концы.
n Замечание. Сумма градусных мер двух дуг окружностей с общими концами равна 360°.
71.
○ Определение. Вписанным углом называется угол, вершина которого лежит на окружности, а стороны пересекают ее.
○ Определение. Вписанный в окружность угол называется опирающимся на ее дугу, если дуга расположена внутри него, а ее концы лежат на его сторонах.
n Теорема (свойство вписанного угла). Вписанный угол измеряется половиной дуги, на которую он опирается.
n Следствие 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
● Следствие 2. Вписанный угол, опирающийся на диаметр - прямой.
n Теорема (о двух пересекающихся хордах). Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
○ Теорема (N 659). Градусные меры дуг окружности, заключенных между параллельными хордами, равны.
○ Теорема (об угле между касательной и секущей(N 664)). Угол между касательной и секущей, проведенной через точку касания, измеряется половиной дуги, заключенной между ними.
○ Теорема (N 668). Перпендикуляр, проведенный из любой точки окружности к диаметру, есть среднее пропорциональное между отрезками, на которые он делит диаметр.
○ Теорема (о длине касательной и секущей(N 670)). Если АВ - касательная (где В – точка касания), а АP секущая (причем P и Q точки пересечения ее с той же окружностью), то 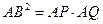 .
.
§ 3. Четыре замечательные точки треугольника.
72.
n Теорема (Свойство биссектрисы угла). Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
● Теорема (обратная к свойству биссектрисы угла). Каждая точка, лежащая внутри угла и равноудаленная от его сторон, лежит на его биссектрисе.
n Следствие (Свойство биссектрис треугольника). Биссектрисы треугольника пересекаются в одной точке.
○ Определение. Серединным перпендикуляром к отрезку называется прямая, проходящая через его середину и перпендикулярная к нему.
● Теорема (Свойство серединного перпендикуляра к отрезку). Каждая точка серединного перпендикуляра к отрезку равноудалена от его концов.
* ● Теорема (обратная к свойству серединного перпендикуляра к отрезку). Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
* n Следствие (Свойство серединных перпендикуляров к сторонам треугольника). Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
73.
n Теорема (Свойство высот треугольника). Высоты треугольника (или их продолжения) пересекаются в одной точке.
○ Определение. Замечательными точками треугольника называются 4 точки: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот (или их продолжений).
§ 4. Вписанная и описанная окружности.
74.
○ Определение. Окружность называется вписанной в многоугольник, если все его стороны касаются этой окружности.
○ Определение. Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности.
○ Теорема (об окружности, вписанной в треугольник). В любой треугольник можно вписать окружность, и притом только одну.
○ Замечание. Не во всякий четырехугольник можно вписать окружность.
● Теорема (свойство описанного четырехугольника). В описанном четырехугольнике суммы противоположных сторон равны.
● Теорема (признак описанного четырехугольника). Если в выпуклом четырехугольнике суммы противоположных сторон равны, то в него можно вписать окружность.
75.
○ Определение. Окружность называется описанной около многоугольника, если все его вершины лежат на этой окружности.
○ Определение. Многоугольник называется вписанным в окружность, если все его вершины лежат на этой окружности.
○ Теорема (об окружности, описанной около треугольника). Около любого треугольника можно описать окружность и притом только одну.
Замечание. Около четырехугольника не всегда можно вписать окружность.
● Теорема (свойство вписанного четырехугольника). Во вписанном четырехугольнике сумма противоположных углов равна 180°.
● Теорема (признак описанного четырехугольника). Если в четырехугольнике сумма противоположных углов равна 180°, то около него можно описать окружность.
○ Теорема (признак ромба (N 696)). Если в параллелограмм можно вписать окружность, то это - ромб.
○ Теорема (свойство ромба (N 700)). В любой ромб можно вписать окружность.
○ Теорема (N 697). Площадь описанного многоугольника равна половине произведения его периметра на высоту.
○ Теорема (признак прямоугольника (N 709)). Если около параллелограмма можно описать окружность, то это - прямоугольник.
○ Теорема (признак равнобедренной трапеции(N 710)). Если около трапеции можно описать окружность, то она - равнобедренная.
Date: 2015-07-02; view: 1763; Нарушение авторских прав