Глава 9

Векторы

§ 1. Понятие вектора.

76.

● Определение. Вектором или направленным отрезком называется отрезок, для которого указано, какой из его концов считается началом, а какой - концом.

○ Определение. Нулевым вектором называется любая точка плоскости.

○ Определение. Длиной ненулевого вектора называется длина соответствующего отрезка; длина нулевого вектора считается равной 0.

77.

 Определение. Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.

 Определение. Нулевой вектор считается коллинеарным любому вектору.

○ Определение (из 10 класса!) Два луча называются сонаправленными, если

1) они параллельны и лежат по одну сторону от прямой, проходящей через их начала, или

2) они совпадают или один из них содержит другой.

○ Определение. Два ненулевых вектора 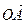и 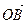называются сонаправленными, если они коллинеарны и при этом лучи ОА и ОВ сонаправлены.

○ Определение. Два ненулевых вектора называются противоположно направленными, если они коллинеарны и не сонаправлены.

○ Замечание. Нулевой вектор сонаправлен с любым вектором.

n Определение. Векторы называются равными, если они сонаправлены и их длины равны.

78.

○ Теорема. От любой точки можно отложить вектор, равный данному, и притом только один.

§ 2. Сложение и вычитание векторов.

79.

○ Определение. Суммой двух векторов называется вектор, полученный из них по правилу треугольника.

 Теорема (правило треугольника). Для любых трех точек А, В и С имеет место равенство .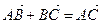

○ Теорема. Для любого вектора 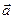справедливо равенство .

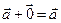80.

n Теорема (законы сложения векторов). Для любых векторов 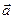, 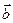и 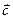справедливы равенства:

1. 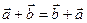(переместительный закон);

2. 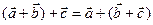(сочетательный закон).

81.

 Теорема (правило многоугольника). Если 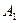, , 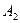…, 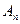- произвольные точки плоскости, то .

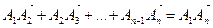82.

○ Определение. Разностью векторов 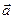и 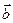называется вектор, сумма которого с вектором 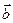равна вектору .

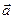○ Определение. Два ненулевых вектора называются противоположными, если они противоположно направлены и их длины равны.

 Замечание. Вектором противоположным нулевому вектору, считается нулевой вектор.

n Теорема. Для любых векторов 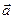и 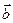справедливо равенство .

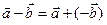§ 3. Умножение вектора на число.

83.

○ Определение. Произведением ненулевого вектора 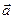на число k называется вектор 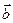, длина которого равна 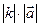, причем вектор 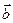сонаправлен вектору 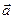при и противоположно направлен при k <0.

○ Определение. Произведением нулевого вектора на любое число считается нулевой вектор.

○ Следствие 1. Произведение любого вектора на число 0 есть нулевой вектор.

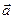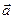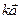○ Следствие 2. Для любого вектора и любого числа k векторы и коллинеарны.

● Теорема (законы умножения вектора на число). Для любых векторов 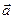, 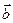и любых чисел k, l справедливы равенства:

1. 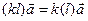(сочетательный закон).

2. 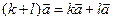(первый распределительный закон).

3. 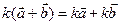(второй распределительный закон).

84.

○ Теорема. Если точка С - середина отрезка АВ, а О - произвольная точка плоскости, то .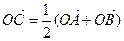

○ Теорема (свойство трапеции). Прямая, проведенная через середины оснований трапеции, проходит через точку пересечения продолжений боковых сторон.

85.

 Определение. Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.

n Теорема (свойство средней линии трапеции). Средняя линия трапеции параллельна основаниям и равна их полусумме.

○ Теорема (N 780). Для любого вектора 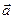справедливо равенство: .

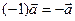○ Теорема (N 797). Средняя линия трапеции проходит через середины диагоналей.

○ Теорема (801). Для любых векторов 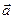и 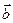справедливы неравенства:

.

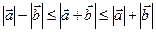○ Теорема (806). Если точка С делит отрезок АВ в отношении m:n, считая от точки А, а О - произвольная точка плоскости, то .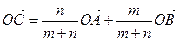

*****

Date: 2015-07-02; view: 628; Нарушение авторских прав