Решение. Для решения данного неравенства воспользуемся методом интервалов

Для решения данного неравенства воспользуемся методом интервалов. Вспомним, что дробь может поменять знак лишь в тех точках, в которых или числитель или знаменатель дроби обращается в ноль. Конечно, для данного неравенства не получится применить правило чередования знаков, как это делается с обычной рациональной дробью, поэтому на каждом из интервалов знак будем проверять отдельно.

Итак, нули знаменателя:

.

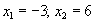Для нахождения нулей числителя решим уравнение:

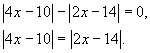
Решить данное уравнение проще всего можно, возведя в квадрат обе части уравнения. Это возведение не приведет к появлению посторонних решений, так как обе части уравнения положительны.

Имеем

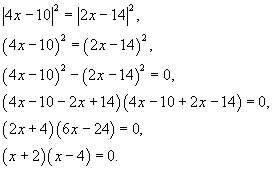
Таким образом, нулями числителя являются .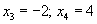

Полученные четыре значения переменной x разбивают числовую прямую на промежутки. Обозначим их на рисунке.

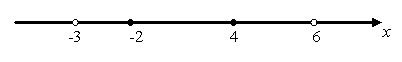
Точк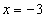и и 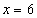выкалываются, так как в этих точках знаменатель обращается в ноль. Точки -2 и 4 закрашиваются и включаются в множество решений неравенства, так как неравенство нестрогое.

Теперь на каждом из интервалов выбираем точку и определяем знак выражения 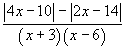в этой точке.

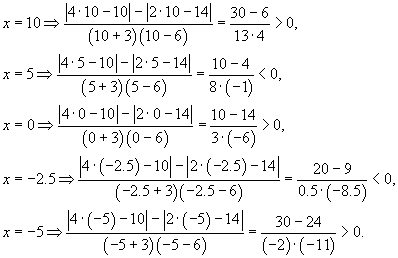
На основании проведенных расчетов расставляем знаки неравенства:

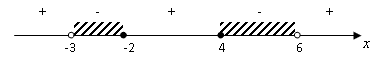
Записываем решение неравенства: .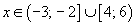

Выписываем целые решения неравенства: 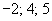. Их сумма равна 7.

Ответ: 7

Задача В10. Куб вписан в правильную четырехугольную пирамиду так, что четыре его вершины находятся на боковых ребрах пирамиды. А четыре другие вершины – на ее основании. Длина стороны основания пирамиды равна 2, высота пирамиды – 6. Найдите площадь S поверхности куба. В ответ запишите значение 4S.

Date: 2015-07-17; view: 380; Нарушение авторских прав