Решение. Пусть - первый член исходной геометрической прогрессии

Пусть 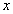- первый член исходной геометрической прогрессии.

Тогда второй член прогрессии - 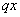, а третий - 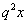, где 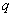- знаменатель прогрессии.

После уменьшения на 8 второго члена, исходный ряд чисел принимает вид:

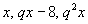
По условию эти числа также составляют геометрическую прогрессию. Пусть 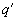- знаменатель этой прогрессии. Тогда должно выполняться равенство: 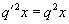(мы выразили третий член новой прогрессии через первый член 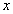и знаменатель ).

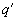Из записанного уравнения после сокращения на 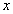и извлечения квадратного корня получаем:

.

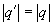Так как по условию 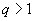, то .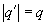

Это значит, что либо 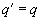, либо .

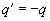Очевидно, выполнение первого равенства невозможно, так как в этом случае для второго члена новой прогрессии можно было бы записать:

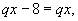
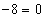- противоречие.

Значит .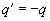

Выразим второй член новой прогрессии через первый при данном условии:

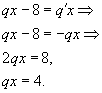
После уменьшения третьего члена новой прогрессии на 25 получаем ряд:

.

Так как по условию этот ряд составляет арифметическую прогрессию, то

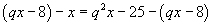(мы нашли разность прогрессии двумя способами и приравняли их).

Учитывая, что 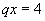, получаем:

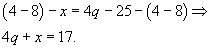
Составляем и решаем систему из двух уравнений:

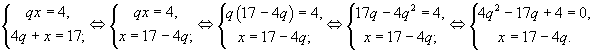
Первое уравнение итоговой системы является квадратным. Его решаем через дискриминант:

Тогда

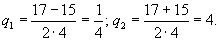
Так как по условию 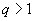, то нам подходит лишь второй корень. Таким образом, .

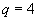Тогда из второго уравнения системы получаем первый член исходной прогрессии:

.

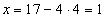Записываем первые три члена прогрессии:

1, 4, 16.

Их сумма равна 21.

Ответ: 21.

Задача В7. Найдите произведение суммы корней уравнения 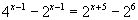на их количество.

Date: 2015-07-17; view: 479; Нарушение авторских прав