Решение. Преобразуем уравнение, используя формулу двойного аргумента для синуса в левой части:

Преобразуем уравнение, используя формулу двойного аргумента для синуса в левой части:

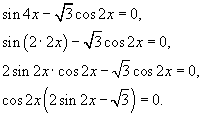
Далее вспоминаем магическую фразу: «Произведение может равняться нулю только тогда, когда хотя бы один из сомножителей равен нулю».

Получаем совокупность двух уравнений:

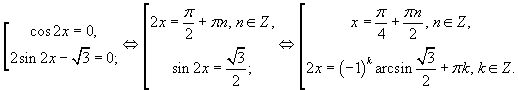
Так как 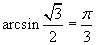, то

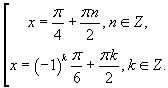
Из условия задачи следует, что необходимо найти самые близкие к нулю корни уравнения. Так как n и k могут принимать любые целые значения, то, вообще, корней исходного уравнения существует бесконечное множество. Поэтому проще всего ответить на вопрос задачи можно следующим образом: перебрать все корни, близкие к нулю, и выбрать из них наибольший и наименьший.

Для этого составим таблицу:

n	-1			k			-1	-2

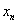
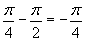
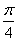
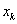
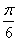
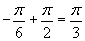
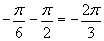
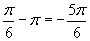
Очевидно, что при остальных n и k ближе к нулю мы уже не подойдем.

Итак, из приведенных значений наименьшим положительным является 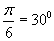, а наибольшим отрицательным - .

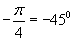Сумма полученных углов равна -15.

Ответ: -15.

Задача В6. Три числа составляют геометрическую прогрессию, в которой 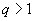. Если второй член прогрессии уменьшить на 8, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 25, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.

Date: 2015-07-17; view: 515; Нарушение авторских прав