
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Усеченное нормальное распределение
|
|
Усеченным нормальным распределением называется распределение, получаемое из классического нормального при ограничении интервала возможных значений наработки до отказа.
Известно, что корректность использования классического нормального распределения наработки достигается при Т ≥ 3 S.
При малых значениях Т и большом S может возникать ситуация, когда функция f (t) «покрывает» своей левой ветвью область отрицательных наработок (рисунок 4.7).
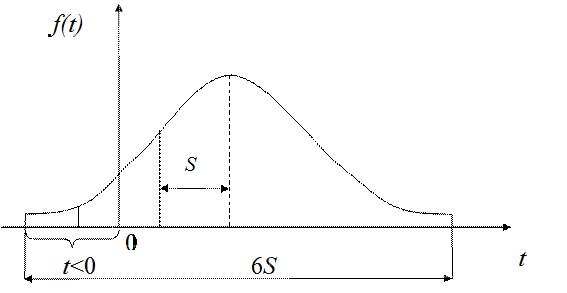
Рис. 4.7 Функция плотности вероятности усеченного нормального распределения
Таким образом, нормальное распределение, являясь общим случаем распределения случайной величины в диапазоне (– ∞; +∞), лишь в частности (при определенных условиях) может быть использовано для моделей надёжности.
В общем случае усечение может быть:
левым – (0; +∞);
двусторонним – (t 1, t 2).
Для рассмотрения количественных характеристик надёжности при усеченном нормальном распределении вводится нормирующий множитель, чтобы сохранить условие нормирования плотности вероятности:
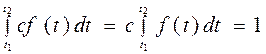 , (4.19)
, (4.19)
где
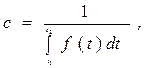
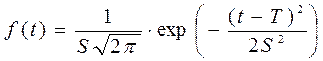 , (4.20)
, (4.20)

откуда
переходя от случайной величины Т = { t } к величине X = { x }:
x 2 = (t 2 –Т) /S, x 1 = (t 1 – Т) /S,
|
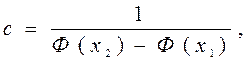 получают
получают 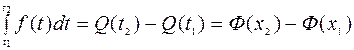 ,
,
откуда:
где Ф (х) – интеграл Лапласа

Усеченный нормальный закон распределения применяется для описания постепенных отказов объектов, что характерно для «стареющих» объектов.
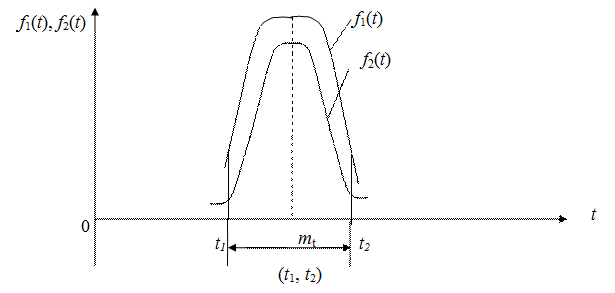
Поскольку [ Ф (x 2) –Ф (x 1)] < 1, то c > 1, поэтому f 1(t) > f 2(t). Здесь f 1(t) – функция плотности распределения отказов для нормального закона распределения, f 2(t) – функция плотности распределения отказов для усеченного нормального закона распределения. Кривая f 1(t) выше, чем f 2(t), так как площади под кривыми f 1(t) и f 2(t) одинаковы и равны 1 (рис. 4.8):
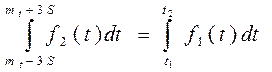
(с погрешностью ≤ 1%)



 Контрольные вопросы
Контрольные вопросы
1 Почему распределение Гаусса называется нормальным?
2 Поясните на изменении кривой плотности распределения отказов влияние параметров распределения: математического ожидания и дисперсии.
3 При каких условиях правильно использовать классическое нормальное распределение, а при каких – усечённое нормальное распределение?
Date: 2015-07-17; view: 5289; Нарушение авторских прав