Гамма-распределение

Гамма-распределение времени безотказной работы описывает схему непрерывного, постепенного износа, при котором отказ не наступает вследствие первого же повреждения, а является следствием накопления повреждений. Каждое из этих повреждений происходит по схеме мгновенного повреждения.

Граничными условиями применения гамма-распределения являются следующие:

· средняя скорость износа устройства постоянна;

· средняя скорость износа подвержена случайным вариациям;

· начальное качество исследуемых устройств полно­стью однородно.

Случайная величина наработки до отказа T имеет гамма-распределение с параметрами α (масштабный параметр) и β (параметр формы), где 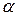, > 0, причём 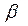– целое число, если функция плотности распределения описывается выражением:

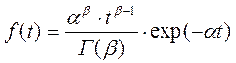, (4.29)

где Г (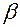) = ( 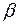– 1)! – гамма-функция Эйлера.

Очевидно, что при 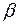=1 выражение (4.29) упрощается до вида 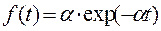, соответствующего экспоненциальному распределению.

Гамма-распределение наиболее хорошо описывает распределение суммы независимых случайных величин, каждая из которых распределена по экспоненциальному закону.

При больших значениях 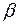гамма-распределение сходится к нормальному распределению с параметрами: , .

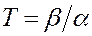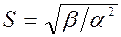Графики изменения показателей надежности при гамма-распределении приведены на рисунке 4.10.

Числовые характеристики наработки до отказа:

- средняя наработка (математическое ожидание наработки) до отказа

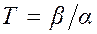, (4.30)

- дисперсия наработки до отказа

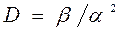. (4.31)

4.3.5 Распределение Вейбулла - Гнеденко

Распределение Вейбулла – Гнеденко довольно универсально, охватывает путем варьирования параметров широкий диапазон случаев изменения вероятностей. Наряду с логарифмическим нормальным распределением оно удовлетворительно описывает наработку деталей по усталостным разрушениям, наработку до отказа подшипников, радиодеталей. Используется для оценки надежности деталей и узлов машин, в частности автомобилей, подъемно-транспортных и других машин. Применяется также для оценки надежности по приработочным отказам.

Распределение характеризуется следующей функцией вероятности безотказной работы:

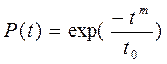. (4.32)

(Здесь t₀ – значение времени, при котором плотность вероятности максимальна, в теории вероятности носит название мода).

Интенсивность отказов

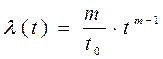. (4.33)

Плотность распределения

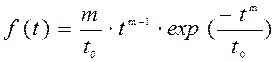. (4.34)

Из формул (4.33) и (4.34) видно, что распределение Вейбулла - Гнеденко имеет два параметра: параметр формы m >1 и параметр масштаба t₀.

Математическое ожидание и среднее квадратическое отклонение рассчитываются соответственно по формулам:

, (4.35)

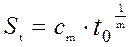, (4.36)

где b_m и с_m – коэффициенты, выбираемые по таблице 4.4

Коэффициенты для расчёта параметров m_t и S_t

Таблица 4.4

Параметр формы m	1/m	bm	сm	Коэффициент вариации
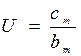
0,400	2,5	3,32	10,4	3,14
0,455	2,2	2,42	6,22	2,57
0,500	2,0	2,00	4,47	2,24
0,556	1,8	1,68	3,26	1,94
0,625	1,6	1,43	2,39	1,67
0,833	1,2	1,10	1,33	1,21
1,2	0,833	0,941	0,787	0,837
1,6	0,625	0,897	0,574	0,640
2,0	0,500	0,887	0,463	0,523
2,5	0,400	0,886	0,380	0,428

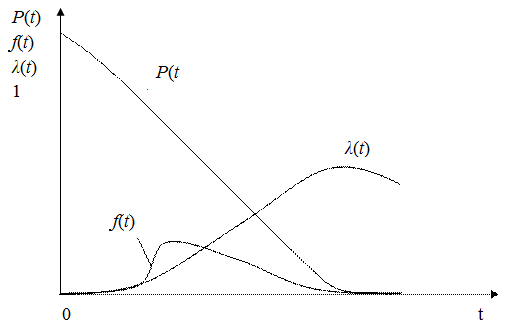
Возможность и универсальность распределения Вейбулла-Гнеденко видны из следующих пояснений (рис. 4.11).

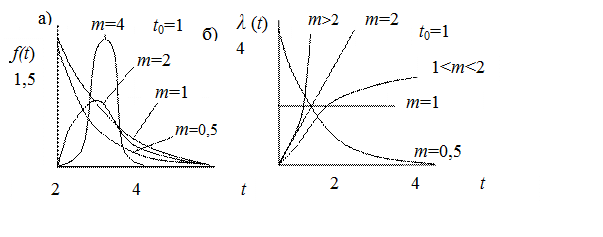
При m < 1 функции λ (t) и f (t) наработки до отказа убывающие.

При m = 1 распределение превращается в экспоненциальное λ (t) = const

и f (t) – убывающая функция.

При m > 1 функция f (t) – одновершинная, функция λ (t) непрерывно возрастающая при 1 < m < 2 с выпуклостью вверх, а при m > 2 – с выпуклостью вниз.

При m = 2 функция λ (t) является линейной и распределение Вейбулла -Гнеденко превращается в распределение Релея.

При m = 3,3 распределение Вейбулла - Гнеденко близко к нормальному.

Кроме рассмотренных законов распределения в качестве моделей надёжности объектов могут использоваться и другие, например, распределение Релея, распределение Эрланга и т. п.

Контрольные вопросы

1 Перечислить виды распределений, описывающих надёжность в период постепенных отказов.

2 Для описания надёжности каких объектов используется логарифмически нормальное распределение?

3 Какой из параметров в выражении плотности распределения отказов при гамма-распределении наработки является параметром формы, а какой –

параметром масштаба?

Date: 2015-07-17; view: 1766; Нарушение авторских прав