Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Числовые характеристики случайных величин
|
|
1. Математическое ожидание - характеристика центра группирования случайных величин:
– для дискретных случайных величин:
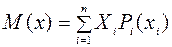 (2.27)
(2.27)
– для непрерывных случайных величин:
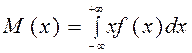 (2.28)
(2.28)
2. Дисперсия есть сумма произведений квадратов разностей случайных величин и математических ожиданий
– для дискретных случайных величин:
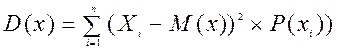 (2.29)
(2.29)
– для непрерывных случайных величин:
 (2.30)
(2.30)
3. Среднее квадратическое отклонение:
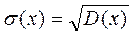 (2.31)
(2.31)
4. Коэффициент вариации:
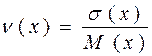 (2.32)
(2.32)
если: n (х) < 0,1 – малое значение коэффициента;
0,1 … 0,33 – среднее значение коэффициента;
n (х) > 0,33 – большое значение коэффициента.
Свойства математического ожидания:
М (ах) = аМ (х), а = const;
М (а+х) = а + М (х);
М (х±у) = М (х) ± М (у);
М (ху) = М (х) × М (у);
М (х2) = (М(х)) 2 + D (х)
Свойства дисперсии:
D (ах) = а2D (х), а = const
D (а + х) = D (х)
D (х ± у) = D (х) ± D (у)
D (х2) = М (х4) - [(М(х)) 2 + d (х) 2 ]
Пример 2.1. Закон распределения случайной величины задан в виде таблицы:
Таблица 2.2
| х | |||
| Р (х) | 0,3 | 0,5 | 0,2 |
Определить числовые характеристики случайных величин.
Решение:
М (х) = 1´0,3 + 2´0,5+ 5´ 0,2= 2,3
D (х) = (1 – 2,3) 2 ´ 0,3 + (2 – 2,3)2 ´ 0,5 + (5 – 2,3)2 ´ 0,2» 2
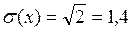
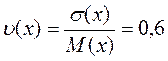
Пример 2.2: Функция распределения имеет вид:
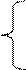 0, при х £ 0
0, при х £ 0
f (x) = 2 х, при 0 < x £ 1
0, при х > 1
Оценить количественно, что вероятность примет значение из диапазона (0,5; 1). Какова вероятность попадания случайной величины в диапазон (0,5; 1) при условии, что событие не появится.
Решение:
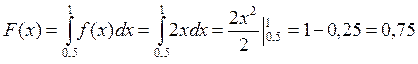
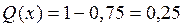
Контрольные вопросы и задачи
1. Почему надёжность необходимо рассматривать в вероятностном аспекте?
2. Как можно подсчитать вероятность безотказной работы через число отказавших объектов и общее число объектов?
3. Какими способами задаются случайной величины?
4. Перечислите и поясните основные теоремы вероятности.
5. Назовите следствия основных теорем теории вероятностей.
6. Закон распределения случайной величины задан в виде таблицы
Таблица 2.3
| Х | -2 | а | ||
| Р | 0,2 | 0,1 | 0,4 | 0,3 |
Известно, что M (x)=0
Найти D (x), a, 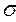 (x), r (x), M (x2).
(x), r (x), M (x2).
7. Функция распределения имеет вид:
 0, при x
0, при x 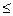 0
0
f (x) = e 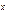 , при 0
, при 0 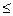 x
x 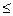 1/2
1/2
x 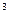 , при ½< x
, при ½< x 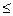 1
1
0, при x >1
Найти вероятность того, что вероятность примет значение из диапазона
(1/3; 2/3).
8. Прибор работает в двух режимах: «1» и «2». Режим «1» наблюдается в 60% случаев, режим «2» – в 40% случаев за время работы T. В режиме «1» прибор отказывает с вероятностью, равной 0,3, а в режиме «2» с вероятностью 0,5. Определить вероятность отказа прибора за время T. Ответ: 0,38.
9. Прибор состоит из 3-х блоков, которые независимо друг от друга могут отказать. Отказ каждого из блоков приводит к отказу всего прибора. Вероятность того, что за время T работы прибора откажет первый блок, равна 0,15, второй – 0,25, третий – 0,1. Найти вероятность того, что за время T прибор проработает безотказно.
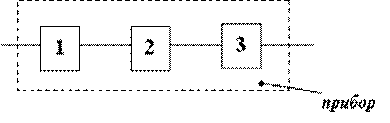

Ответ: 0,57375
10. Прибор состоит из 2-х блоков, дублирующих друг друга. Вероятность того, что за время T каждый из блоков проработает безотказно, равна 0,9. Отказ прибора произойдет при отказе обоих блоков. Найти вероятность того, что за время T прибор проработает безотказно.
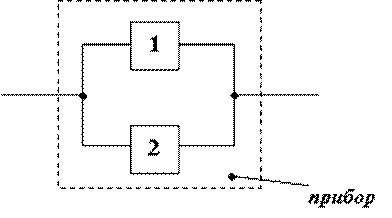
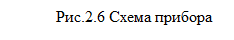
Ответ: 0,99.
3 Показатели надёжности объекта
Безотказность и другие свойства надёжности проявляются через случайные величины: наработку до отказа (наработку между отказами) и количество отказов за заданное время. Поэтому количественными характеристиками здесь выступают вероятностные переменные.
Наработка – продолжительность (объём) работы объекта. Измеряется в любых неубывающих величинах (единица времени, число циклов нагружений, километры пробега и т. п.). Объект может работать непрерывно (с учётом перерывов на ремонт) или с перерывами, независящими от технического состояния (в этом случае различаются непрерывная и суммарная наработка).
Появление отказов не предопределено заранее, случайно, поэтому теория надежности основана на математическом аппарате теории вероятностей и математической статистики.
Для оценки надёжности проводятся эксплуатационные испытания значительного числа N элементов в течение времени t. Пусть к концу испытаний остается Nр работоспособных элементов и n отказавших.
Тогда относительное количество отказов:
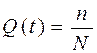 . (3.1)
. (3.1)
Вероятность безотказной работы оценивается относительным количеством работоспособных элементов:
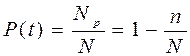 . (3.2)
. (3.2)
Вероятность безотказной работы (ВБР) означает, что в пределах заданной наработки отказ объекта не возникнет.
Так как безотказная работа и отказ – взаимно противоположные события, то сумма их вероятностей равна единице:
P (T) + Q (t) = 1,
 = F (t).
= F (t).
F (t) есть интегральная функция распределения случайной наработки t.
Так как события, заключающиеся в том, что наступил или не наступил отказ к моменту наработки t, являются противоположными, то нетрудно убедиться, что P (t) является убывающей, а Q (t) – возрастающей функцией наработки. Действительно, а) в момент начала испытаний t = 0 число работоспособных объектов равно общему их числу N (t) = N (0) = N, а число отказавших –
n (t) = n (0) = 0, поэтому P (t) = P (0) = 1, а Q (t) = Q (0) = 0;
б) при наработке t  ∞ все объекты, поставленные на испытания, откажут, то есть
∞ все объекты, поставленные на испытания, откажут, то есть
N (∞) = 0, а n (∞) = N, поэтому P (t) = P (∞) = 0, а Q (t) = Q (∞) = 1.
Вероятность безотказной работы есть количественная мера того, что случайная величина наработки до отказа T окажется не меньше некоторой заданной наработки t, если t ≥0:
P (t) = P { T ≥t }. (3.3)
Очевидно, что Q (t) является функцией распределения случайной величины T и представляет собой вероятность того, что наработка до отказа окажется меньше некоторой заданной наработки t:
Q (t) = P { T < t }. (3.4)

Рис. 3.1 Изображения функций P (t) и Q (t)
Пример 3.1 Найти P (t) в интервале наработки [ t, t +∆t ] при условии, что объект безотказно проработал до начала t интервала.
Решение:
Вероятность определяется посредством использования теоремы умножения вероятностей и выделения следующих событий:
A = {безотказная работа объекта до момента t };
B = {безотказная работа объекта в интервале ∆t };
C = A·B = {безотказная работа объекта до момента t +∆t }.
Очевидно P(C) = P (A·B) = P (A) ·P (B| A), поскольку события A и B будут зависимыми.
Условная вероятность P (B/A)представляет P (t, t+∆t) в интервале [ t, t + ∆t ], поэтому
P (B / A) = P (t, t + ∆t) = P (C) / P (A) = P (t + ∆t) / P (t). (3.5)
Q (t) в интервале наработки [ t, t + ∆t ], с учётом (3.5), равна:
Q (t, t + ∆t) = 1 – P (t, t + ∆t) = [ P (t) – P (t + ∆t)] / P (t). (3.6)
Для невосстанавливаемых объектов применяется понятие наработка до отказа (он же является и последним отказом).
Средняя наработка до отказа Т 1 вычисляется по формуле:
 ,
,
где F (t) – функция распределенпия наработки до отказа;
Р (t) – вероятность безотказной работы;
f (t) – плотность распределения наработки до отказа.
Статистически средняя наработка до отказа определяется по формуле:
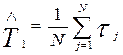 ,
,
где N –число работоспособных объектов при t =0
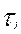 – наработка до первого отказа каждого из объектов.
– наработка до первого отказа каждого из объектов.
Для восстанавливаемых объектов понятие применяется наработка на отказ (наработка между двумя соседними во времени отказами). После каждого
отказа производится восстановление работоспособного состояния.
Характеристикой безотказности случайной наработки Т является математическое ожидание, которое называется средней наработкой на отказ (между отказами) [48]
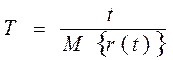 , (3.7)
, (3.7)
где t – суммарная наработка, r (t) – число отказов, наступивших в течение этой наработки, М { r (t)} – математическое ожидание этого числа. В общем случае средняя наработка на отказ оказывается функцией t.
Статистическая оценка средней наработки на отказ Т есть величина, рассчитываемая по формуле:
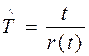 , (3.8)
, (3.8)
в отличие от формулы (3.7) здесь r (t) — число отказов, фактически происшедших за суммарную наработку t.
Статистическая вероятность отказов
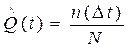 ,
,
где n (D t) – количество отказов;
N – число взятых на испытания объектов.
Статистическая частота отказов
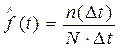 , (3.9)
, (3.9)
где D t – данный интервал времени.
Длядифференцируемых функций распределения случайной величины определяется первая производная, называемая плотностью распределения (законом распределения) времени работы объекта до отказа:
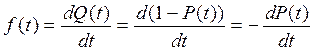 . (3.10)
. (3.10)
Интенсивность отказов как статистический параметр – отношение числа отказавших объектов в единицу времени к числу объектов, продолжающих безотказно работать в данный промежуток времени:
 , (3.11)
, (3.11)
где Δ n (Δt)– число отказавших объектов за промежуток времени от
(t -Δ t/ 2)до (t +Δ t/ 2),
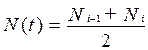
 , (3.12)
, (3.12)
где Ni-1 – число исправно работающих объектов в начале интервала Δ t,
Ni – число исправно работающих объектов в конце интервала Δ t.
Интенсивность отказов показывает, какая часть объектов выходит из строя в единицу времени относительно среднего числа исправно работающих объектов.
Интенсивность отказов как вероятностный параметр – условная плотность вероятности возникновения отказа изделия при условии, что до рапссматриваемого момента t отказ не возник:
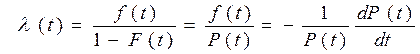 , (3.13)
, (3.13)
где функции f (t) и λ (t) измеряются в ч  .
.
При интегрироавнии (3.10) получается:
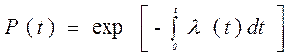 . (3.14)
. (3.14)
Величина λ (t) dt есть вероятность того, что элемент, безотказно проработавший в интервале наработки [0, t ], откажет в интервале [ t, t + dt ].
Выражение (3.13), называемое основным законом надежности, позволяет установить временное изменение вероятности безотказной работы при любом характере изменения интенсивности отказов во времени.
В частном случае постоянства интенсивности отказов λ (t) = 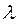 = const выражение (3.13) преобразуется в известное в теории вероятностей экспоненциальное распределение
= const выражение (3.13) преобразуется в известное в теории вероятностей экспоненциальное распределение
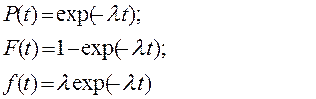

3.1 Показатели надёжности восстанавливаемых объектов
Работоспособность определяется параметрами:
· Вероятность безотказной работы Р (t).
· Средняя наработка на отказ Т.
· Параметр потока отказов μ (t).
· Среднее время восстановления Т В.
Параметр потока отказовμ (t)есть отношение математического ожидания числа отказов восстанавливаемого объекта за достаточно малую его наработку к значению этой наработки определяется по формуле: 
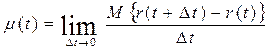 , (3.16)
, (3.16)
где  – матемктическое ожидание,
– матемктическое ожидание, 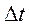 – малый отрезок наработки, r(t) –число отказов, наступивших отначального момента времени до достижения наработки t,
– малый отрезок наработки, r(t) –число отказов, наступивших отначального момента времени до достижения наработки t, 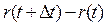 –число отказов на отрезке
–число отказов на отрезке 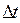 .
.
При расчетах и обработке экспериментальных данных применяют осредненный параметр потока отказов
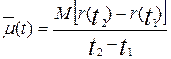 , (3.17)
, (3.17)
здесь 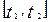 – конечный отрезок времени, на котором определяется число отказов, причем
– конечный отрезок времени, на котором определяется число отказов, причем 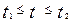 . Для стационарного потока отказов параметры, определяемые по формулам не зависят от t.
. Для стационарного потока отказов параметры, определяемые по формулам не зависят от t.
Cтатистическая оценка параметра потока отказов делается по формуле, которая аналогична формуле (3.16):
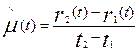 (3.18)
(3.18)
Параметр потока отказов представляет собой плотность вероятности возникновения отказа восстанавливаемого объекта. Отказы объектов возникают в случайные моменты времени, и в течение заданного периода эксплуатации наблюдается поток отказов.
Существует множество математических моделей потоков отказов. Наиболее часто при решении задач надежности электроустановок используют простейший поток отказов - пуассоновский поток. Простейший поток отказов удовлетворяет одновременно трем условиям: стационарности, ординарности, отсутствия последствия.
Стационарность случайного процесса (времени возникновения отказов) означает, что на любом промежутке времени Δ ti вероятность возникновения n отказов зависит только от n и величины промежутка Δ ti, но не зависит от сдвига Δ ti по оси времени. Следовательно, при 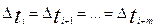 вероятность появления n отказов по всем интервалам составит
вероятность появления n отказов по всем интервалам составит
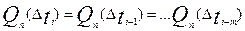 . (3.19)
. (3.19)
Ординарность случайного процесса означает, что отказы являются событиями случайными и независимыми. Ординарность потока означает невозможность появления в один и тот же момент времени более одного отказа, то есть
при n >1  . (3.20)
. (3.20)
Отсутствие последствия означает, что вероятность наступления n отказов в течение промежутка Δ ti не зависит от того, сколько было отказов и как они распределялись до этого промежутка. Следовательно, факт отказа любого элемента в системе не приведет к изменению характеристик (работоспособности) других элементов системы, если даже система и отказала из-за какого-то элемента.
Опыт эксплуатации сложных технических систем показывает, что отказы элементов происходят мгновенно и если старение элементов отсутствует
(l = const), то поток отказов в системе можно считать простейшим.
Случайные события, образующие простейший поток, распределены по закону Пуассона:
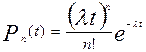 при
при  n і ³ 0 (3.21)
n і ³ 0 (3.21)
где Рn(t) – вероятность возникновения в течение времени t ровно n событий (отказов); l – параметр распределения, совпадающий с параметром потока событий.
Если в выражении (2.16) принять n = 0, то получится 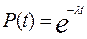 – вероятность безотказной работы объекта за время t при интенсивности отказов
– вероятность безотказной работы объекта за время t при интенсивности отказов
l = const. Нетрудно доказать, что если восстанавливаемый объект при отсутствии восстановления имеет характеристику l = const, то, придавая объекту восстанавливаемость, следует записать μ (t) = const; l = μ.
Это свойство широко используется в расчётах надёжности ремонтируемых устройств. Например, важнейшие показатели надежности оборудования электроустановок даются в предположении, что потоков отказов и восстановлений являются простейшими, когда 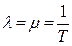 и, соответственно,
и, соответственно,
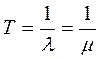 . (3.22)
. (3.22)
Среднее время восстановления Т В:
 , (3.23)
, (3.23)
где n – число отказов объекта;
ТВi – время, затраченное на отыскание и устранение одного отказа.
Функция распределения:
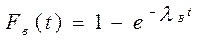 , (3.24)
, (3.24)
где 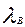 – интенсивность восстановления работоспособности объекта; характеризует среднее число восстановлений ремонтируемого объекта в единицу времени,
– интенсивность восстановления работоспособности объекта; характеризует среднее число восстановлений ремонтируемого объекта в единицу времени,
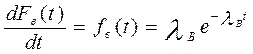 . (3.25)
. (3.25)
Интенсивность восстановления работоспособности объекта:
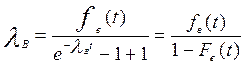 . (3.26)
. (3.26)
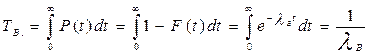 , (3.27)
, (3.27)
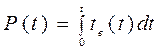 (3.28)
(3.28)
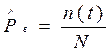 , (3.29)
, (3.29)
где n (t) – число восстановленных за время t объектов;
N – общее число отказавших объектов.
Вероятность безотказной работы восстанавливаемого объекта:
Pr (t) – количественная мера того, что объект в заданный момент времени будет работоспособен.
Событие А: объект работоспособен до момента времени t и работоспособен на участке времени D t.
А: Р (t, t+Dt) =Р (t) Р (D t) =Р (t) е-lt
Событие В: объект вышел из строя к моменту времени t, но был восстановлен за период D t. Выражение для события В:
Р (t, t+ D t) = (1-Р (t))(1-е-lDt)
Р (t, t+ D t) =P (t) е-lDt + (1-P (t))(1-е-lDt) (3.30)
Согласно формулам (3.10) … (3.14)
 |
е -lDt = 1-lВ D t??????
преобразуется к виду:
1-е-lDt = lВD t????????
P (t, t+ D t) = P (t)(1-l D t) + (1-Р(t)),
lВ D t=1,
1 = P (t) – P (t) l D t + lВ D t – P (t) lВ D t
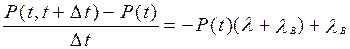

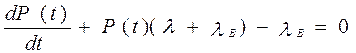 ,
,
Решение этого дифференциального уравнения имеет вид:
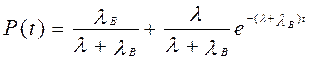 . (3.31)
. (3.31)
Изображение функции P r(t) восстанавливаемого изделия и функции P (t) невосстанавливаемого изделия представлено на рисунке 3.2.
P (t) 
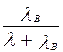
t
рис. 3.2. графики функции Pr (t)и P (t)
Надёжность восстанавливаемого P r(t) изделия всегда выше надёжности невосстанавливаемого изделия P (t).
Пример 3.2. В результате наблюдения за работой редуктора было зарегистрировано 8 отказов, наработки ti составляют в сутках 18, 9, 14, 27, 16, 8, 14, 22. Определить наработку на отказ 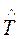 и вероятность его безотказной работы в пределах наработки D t = 20 ч.
и вероятность его безотказной работы в пределах наработки D t = 20 ч.
Решение:
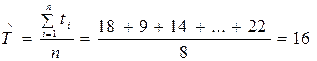 суток
суток
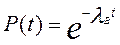

|
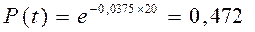 .
.
Date: 2015-07-17; view: 2844; Нарушение авторских прав