Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Совместное действие внезапных и постепенных отказов
|
|
Вероятность безотказной работы изделия за период t, если до этого оно проработало время Т, по теореме умножения вероятностей:
P (t) =Pв (t) Pп (t), (4.37)
где 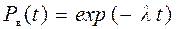 , (4.38)
, (4.38)
и 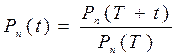 . (4.39)
. (4.39)
– вероятности отсутствия внезапных и постепенных отказов, соответственно. На рисунке 4.12 показаны вероятности отсутствия внезапных отказов и кривая вероятности безотказной работыпри совместном действии внезапных и постепенных отказов.
Вначале, когда интенсивность постепенных отказов низка, кривая P (t) соответствует кривой P в(t), затем резко снижается.
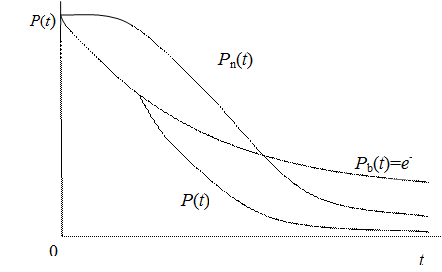 |
 Рис. 4.12 Совместное действие внезапных и постепенных отказов
Рис. 4.12 Совместное действие внезапных и постепенных отказов
4.5 Надёжность восстанавливаемых объектов.
Постановка задачи. Общая расчётная модель
При расчёте показателей надёжности восстанавливаемых объектов и систем наиболее распространено допущение:
· экспоненциальное распределение наработки между отказами;
· экспоненциальное распределение времени восстановления.
Допущение во многом справедливо, поскольку, во-первых, экспоненциальное распределение наработки описывает функционирование системы на участке нормальной эксплуатации, во-вторых, экспоненциальное распределение описывает процесс без «предыстории».
Применение экспоненциального распределения для описания процесса восстановления позволяет при независимых отказах представить анализируемые системы в виде марковских систем.
При экспоненциальном распределении наработки между отказами и времени восстановления расчёт надёжности производится методом дифференциальных уравнений для вероятностей состояний (уравнений Колмогорова-Чепмена).
Случайный процесс в какой-либо физической системе S называется марковским (рисунок 4.13), если он обладает следующим свойством: для любого момента t0 вероятность состояния системы в будущем (t > t0) зависит только от состояния в настоящем (t = t0) и не зависит от того, когда и каким образом система пришла в это состояние (иначе: при фиксированном настоящем будущее не зависит от предыстории процесса – прошлого).
t < t 0 t > t 0
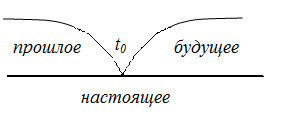

Для марковского процесса «будущее» зависит от «прошлого» только через «настоящее», то есть будущее протекание процесса зависит только от тех прошедших событий, которые повлияли на состояние процесса в настоящий момент.
Марковский процесс, как процесс без последействия, не означает полной независимости от прошлого, поскольку оно проявляется в настоящем.
В общем случае для системы S необходимо иметь математическую модель в виде множества состояний системы S 1, S 2, …, S n, в которых она может находиться при отказах и восстановлениях элементов.
Для рассмотрения принципа составления модели введены допущения:
· отказавшие элементы системы (или сам рассматриваемый объект) немедленно восстанавливаются (начало восстановления совпадает с моментом отказа);
· отсутствуют ограничения на число восстановлений;
· если все потоки событий, переводящих систему (объект) из состояния в состояние, являются пуассоновскими (простейшими), то случайный процесс переходов будет марковским процессом с непрерывным временем и дискретными состояниями S 1, S 2 , …, S n.
Основные правила составления модели:
1. Модель изображают в виде графа состояний.
Элементы графа:
а) кружки (вершины графа S 1, S 2 , …, S n) – возможные состояния системы S, возникающие при отказах элементов; б) стрелки – возможные направления переходов из одного состояния S iв другое Sj.
Над/под стрелками указываются интенсивности переходов.


«Петлей» обозначаются задержки в том или ином состоянии S 0 и S 1, а именно:
S 0– исправное состояние продолжается;
S 1– состояние отказа продолжается (в дальнейшем петли на графах не рассматриваем).
Граф состояний отражает конечное (дискретное) число возможных состояний системы S 1, S 2, …, S n. Каждая из вершин графа соответствует одному из состояний.
2. Для описания случайного процесса перехода состояний (отказ / восстановление) применяют вероятности состояний P 1(t), P 2(t), …, P i(t), …, P n(t), где P i(t) – вероятность нахождения системы в момент t в i-м состоянии, то есть P i(t) = P { S (t) = S i}.
Очевидно, что для любого t
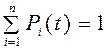 . (4.40)
. (4.40)
3. По графу состояний составляется система обыкновенных дифференциальных уравнений первого порядка (уравнений Колмогорова-Чепмена), имеющих вид:
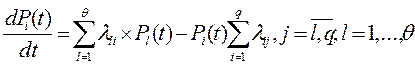 . (4.41)
. (4.41)
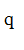
|









|










В общем случае интенсивности потоков λ ij и μ ij могут зависеть от времени t.
При составлении дифференциальных уравнений пользуются простым мнемоническим правилом:
а) в левой части записывается производная по времени t от Pi (t);
б) в правой части число членов равно числу стрелок, соединяющих рассматриваемое состояние с другими состояниями;
в) каждый член правой части равен произведению интенсивности перехода на вероятность того состояния, из которого выходит стрелка;
г) знак произведения положителен, если стрелка входит (направлена острием) в рассматриваемое состояние, и отрицателен, если стрелка выходит из него.
Проверкой правильности составления уравнений является равенство нулю суммы правых частей уравнений.
4. Чтобы решить систему дифференциальных уравнений для вероятностей состояний P1 (t), P2 (t) .… Pi (t), …, Pn (t), необходимо задать начальное значение вероятностей P1 (0), P2 (t),… Pi (0), …, Pn (0); при t = 0 их сумма равна единице:
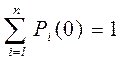
Если в начальный момент t = 0 состояние системы известно, например, S (t= 0) = Si, то Pi (0) = 1, а остальные равны нулю.
4.5.1 Показатели надёжности восстанавливаемых объектов
Все состояния системы S можно разделить на подмножества:
SК 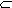 S – подмножество состояний j =
S – подмножество состояний j = 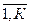 , в которых система работоспособна (читается «S К принадлежит S»);
, в которых система работоспособна (читается «S К принадлежит S»);
SM 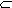 S – подмножество состояний z =
S – подмножество состояний z = 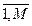 , в которых система неработоспособна.
, в которых система неработоспособна.
S = S K  S M (читается «SК или S M », «S К дизъюнкция S M»),
S M (читается «SК или S M », «S К дизъюнкция S M»),
SK 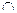 SM = 0 (читается «S К и SM», «SК конъюнкция S M»).
SM = 0 (читается «S К и SM», «SК конъюнкция S M»).
1. Функция готовности Г (t) системы определяет вероятность нахождения системы в работоспособном состоянии в момент t:
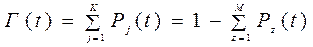 , (4.42)
, (4.42)
где P j(t) – вероятность нахождения системы в работоспособном j -м состоянии;
P z(t)– вероятность нахождения системы в неработоспособном z -м состоянии.
2. Функция простоя П (t) системы:
 (4.43)
(4.43)
3. Коэффициент готовности k г.с . системы определяется при установившемся режиме эксплуатации (при t  ∞). При t
∞). При t  ∞ устанавливается предельный стационарный режим, в ходе которого система переходит из состояния в состояние, но вероятности состояний уже не меняются:
∞ устанавливается предельный стационарный режим, в ходе которого система переходит из состояния в состояние, но вероятности состояний уже не меняются:
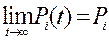 :
: 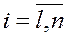 .
.
Коэффициент готовности k г .с. можно рассчитать по системе (4.41) дифференциальных уравнений, приравнивая нулю их левые части dPi (t) /dt = 0, так как Pi = const при t  ∞. Тогда система уравнений (4.41) превращается в систему алгебраических уравнений вида:
∞. Тогда система уравнений (4.41) превращается в систему алгебраических уравнений вида:
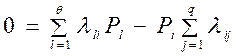 , (4.44)
, (4.44)
и коэффициент готовности
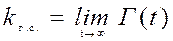 (4.45)
(4.45)
есть предельное значение функции готовности при установившемся режиме t →∞.
4. Параметр потока отказов системы
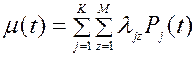 , (4.46)
, (4.46)
где λ jz – интенсивности (обобщенное обозначение) переходов из работоспособного состояния в неработоспособное.
5. Функция потока отказов
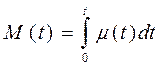 . (4.47)
. (4.47)
6. Средняя наработка между отказами на интервале t
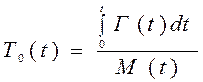 . (4.48)
. (4.48)
Примечание: при t → ∞, когда P j(t) = ∞) = Pj(∞) = P j, средняя наработка между отказами T0= kг.с . / μ, где µ (∞) = µ.
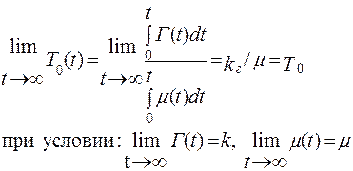
В качестве примера вычисления показателей надежности рассмотрен восстанавливаемый объект, у которого поток отказов простейший (пуассоновский) с параметром потока
μ = λ= 1 / T, (4.49)
а распределение времени восстановления подчиняется экспоненциальному распределению с интенсивностью восстановления
μ = 1 / T В, (4.50)
где T – средняя наработка между отказами; T В – среднее время восстановления.


 Состояния элемента: S 0 – работоспособное; S 1 – неработоспособное; Р 0(t) – вероятность работоспособного состояния при t; P 1(t) – вероятность неработоспособного состояния при t.
Состояния элемента: S 0 – работоспособное; S 1 – неработоспособное; Р 0(t) – вероятность работоспособного состояния при t; P 1(t) – вероятность неработоспособного состояния при t.
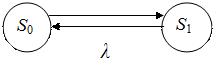
Рис. 4.16 Граф состояний восстанавливаемого объекта
Система дифференциальных уравнений:
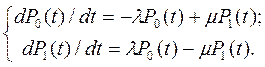 (4.51)
(4.51)
Начальные условия: при t = 0 P 0(t = 0) = P 0(0) = 1; P 1(0) = 0,
поскольку состояния S 0и S 1представляют полную группу событий, то
P 0(t) + P 1(t) = 1. (4.52)
Путём выражения P 0(t) = 1 - P 1(t) и подстановки в (4.51) получено одно дифференциальное уравнение относительно P 1(t):
dP 1(t) /dt = λ (1 – P 1 (t)) – μP 1(t). (4.53)
Решение уравнения производится с использованием преобразования Лапласа. Преобразование Лапласа для вероятностей состояния Pi (t):
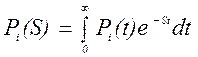 ,
,
где P i(S) = L { P i(t)} – изображение вероятности P i(t).
Преобразование Лапласа для производной dP i(t) /dt:
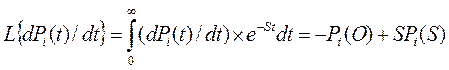
После применения преобразования Лапласа к левой и правой частям уравнения получено уравнение изображений:
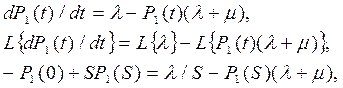
где L { λ } = λ L {1} = λ /S.
При P 1(0) = 0
SP 1(S) + P 1(S)(λ + μ) = λ /S,
P 1(S)(S + λ+μ) = λ /S.
Преобразованием полученных соотношений получено выражение вероятности нахождения объекта в неработоспособном состоянии:
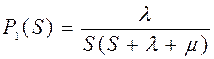 (4.54)
(4.54)
Введение обозначения λ+ μ = а позволяет преобразовать правую часть выражения (4.54) к виду:
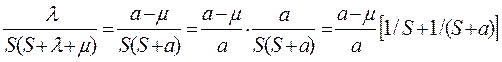 .
.
Применяя обратное преобразование Лапласа, с учётом L { f (t)} = 1 /S, а также f (t) = 1; L { f (t)} = 1 /(S + a), получают f (t) = e-at, после чего находят вероятность пребывания объекта в неработоспособном состоянии в виде выражения:
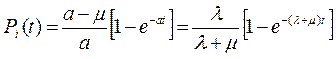 . (4.55)
. (4.55)
Тогда вероятность нахождения в работоспособном состоянии
P 0(t) = 1 – P 1(t), равна:
 . (4.56)
. (4.56)
С помощью полученных выражений можно рассчитать вероятность работоспособного состояния и отказа восстанавливаемого объекта в любой момент t.
Коэффициент готовности системы kг.с. определяется при установившемся режиме t  ∞, при этом P i(t) = P i = const, поэтому составляется система алгебраических уравнений с нулевыми левыми частями, поскольку dP i(t) /dt = 0.
∞, при этом P i(t) = P i = const, поэтому составляется система алгебраических уравнений с нулевыми левыми частями, поскольку dP i(t) /dt = 0.
Так как kг. с есть вероятность того, что система окажется работоспособной в момент t при t  ∞, то из полученной системы уравнений определяется
∞, то из полученной системы уравнений определяется
P 0 = kг .с.,
при t  ∞ алгебраические уравнения имеют вид:
∞ алгебраические уравнения имеют вид:
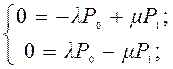 (4.57)
(4.57)
дополнительное уравнение: P 0 + P 1 = 1.
При P 1 = 1 – P 0, получается 0 = λP 0 - μ( 1 - P 0), или μ = P 0 (λ + μ),
откуда
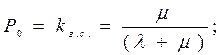 (4.58)
(4.58)
Остальные показатели надежности восстанавливаемого элемента:
· функция готовности Г (t) = P 0(t),
· функция простоя П (t) = 1 – Г (t) = P 1(t),
· параметр потока отказов µ (t) = λP 0(t) = λГ (t),
при t  ∞ (стационарный установившийся режим восстановления)
∞ (стационарный установившийся режим восстановления)
µ (t) = µ (∞) = µ = λP 0 = λkг.с. ;
· ведущая функция потока отказов
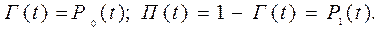
· средняя наработка между отказами t 0 = kг.с./ μ = kг.с. /kг = 1/ λ.
Метод дифференциальных уравнений может быть использован для расчёта показателей надёжности и невосстанавливаемых объектов (систем).
В этом случае неработоспособные состояния системы являются «поглощающими», и интенсивности λ выхода из этих состояний исключаются.
Для невосстанавливаемого объекта граф состояний имеет вид (рис. 4.17).


Система дифференциальных уравнений для данного объекта:
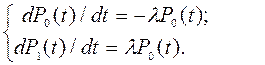
Начальные условия: P 0 (0) = 1; P 1(0) = 0.
Изображение по Лапласу первого уравнения системы:
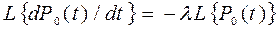 ;
;
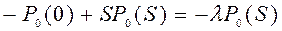 .
.
После группировки:
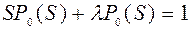 ;
;
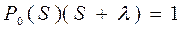 ,
,
откуда 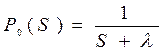 ,
,
используя обратное преобразование Лапласа, оригинал вероятности нахождения в работоспособном состоянии, то есть вероятность безотказной работы к наработке t:
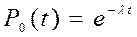 .
.
4.4.2 Связь логической схемы надёжности с графом состояний
Переход от логической схемы к графу состояний необходим:
· при смене методов расчёта надёжности и сравнении результатов;
· для оценки выигрыша в надёжности при переходе от невосстанавливаемой системы к восстанавливаемой.
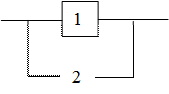
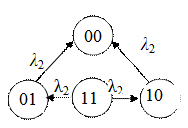
Рассмотрим типовые логические структуры надежности. Типовые соединения рассмотрены для невосстанавливаемых систем (граф – однонаправленный, переходы характеризуются интенсивностями отказов λ).
Для восстанавливаемых систем в графах состояний добавляются обратные стрелки, соответствующие интенсивностям восстановлений l В.
Типовые логические структуры надёжности
Таблица 4.5
| Структурная логическая схема | Графы состояний | ||||
| Элементы различной надёжности | Равнонадёжные элементы | ||||
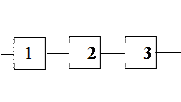
| 
| 
| |||
| 
|
| |||
| 
|  
|
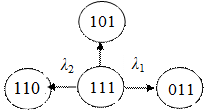
Обозначения на графах состояний:
1 – работоспособное состояние элемента,
0 – неработоспособное состояние элемента.
Контрольные вопросы:
1 В чём особенности Марковского случайного процесса, на основе которого строится расчётная модель для восстанавливаемых объектов и систем?
2 Назовите основные этапы составления расчётной модели.
3 Поясните мнемоническое правило составления дифференциального уравнения вероятностей состояния (уравнение Колмогорова - Чепмена).
4 Дайте определение и поясните смысл показателей надежности восстанавливаемых объектов и систем.
5 Каковы особенности применения метода дифференциальных уравнений для расчета надежности невосстанавливаемых объектов?
6 На любом из примеров поясните связь графа состояний с логической структурой надёжности.
4.6 Пример расчёта безотказности с использованием модели
«прочность – нагрузка»
1. Рассчитать элемент, на который действует растягивающая нагрузка (рис. 4.18).
Принимается, что растягивающая нагрузка Р и предел прочности на растяжение s являются случайными величинами, имеющими нормальный закон распределения вероятностей с параметрами соответственно: Р = 17800 Н, 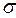 р = 445 МПа и s = 690 МПа,
р = 445 МПа и s = 690 МПа, 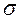 s = 34,5 МПа. Заданное значение безотказности R 3 = 0.9999.
s = 34,5 МПа. Заданное значение безотказности R 3 = 0.9999.
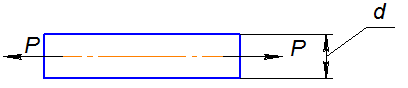

Решение: растягивающее напряжение определяется по формуле:
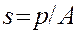 , где А =
, где А = 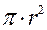 . Допуск на радиус выражается через долю
. Допуск на радиус выражается через долю 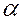 от номинального значения r: 3
от номинального значения r: 3 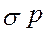 =
= 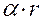 ,
, 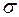 r = (
r = (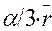 ).
).
По формулам расчета математического ожидания и среднеквадратического отклонения линейной функции случайной величины получается:  =
= 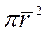 ;
;

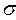 =
= 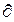
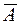 /
/ 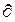 r |r =F
r |r =F 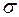 r= 2
r= 2 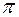
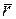
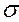 r;
r; 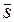 =
=  /
/ 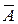 =
= 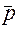 /(
/(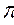
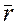 2);
2);
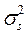 =
= 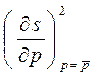 ·
· 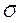 р+
р+ 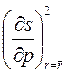 ·
· 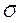 r=
r= 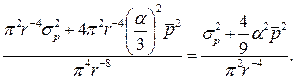
Плотность распределения прочности:
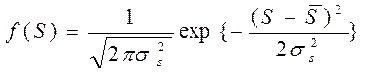 ,
,
плотность распределения нагрузки:
f (s) = 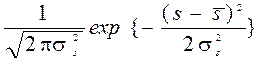 ,
,
плотность распределения разности S-s соответственно имеет вид:
f (S-s)= 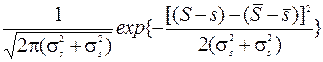 ,
,
условие параметрической безотказности определяется равенством:
R=P { S-s>0 },
статистический запас прочности находится из выражения для Р (S-s):
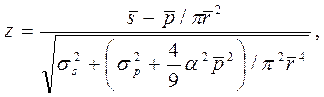
где z − квантиль стандартного нормального распределения.
Для R 3 = 0,9999 по таблицам стандартного нормального распределения находится: z = 3,72. При 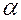 = 0,015 выполняется равенство
= 0,015 выполняется равенство
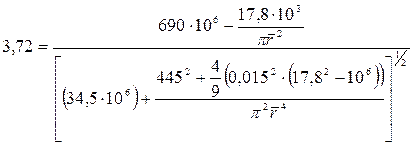 ,
,
откуда 144,6 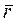 4- 24,6
4- 24,6 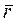 2 + 1 = 0 и окончательно для положительных корней уравнения
2 + 1 = 0 и окончательно для положительных корней уравнения 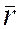 1=2,60 мм;
1=2,60 мм; 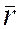 = 3,21 мм соответственно R = 0,00001; R = 0,9999.
= 3,21 мм соответственно R = 0,00001; R = 0,9999.
Влияние допуска 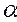 и изменчивости прочности материала на надежность элемента представлено в таблицах 4.6 и 4.7.
и изменчивости прочности материала на надежность элемента представлено в таблицах 4.6 и 4.7.
Влияние допуска на надёжность элемента
Таблица 4.6
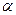 , % , %
| 1,5 | 1,5 | ||
| Z | 3,72 | 3,61 | 3,36 | 3,1 |
| R | 0,9999 | 0,9998 | 0,9996 | 0,999 |
Влияние прочности материала на надёжность
Таблица 4.7
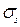 , МПа , МПа
| 34,5 | 41,4 | 48,3 | 55,2 | 62,1 | 68,9 |
| R | 0,9999 | 0,999 | 0,999 | 0,992 | 0,984 | 0,974 |
2. Рассчитать вал, на который действует скручивающая нагрузка Т (рис. 4.19).
Заданное значение безотказности R3 = 0,999. Крутящий момент характеризуется параметрами Т = 11300 Н·м, sT. Допустимое срезающее напряжение ограничивается значениями S, ss. Принимается изменчивость радиуса вала sr = (a/3) ·r.
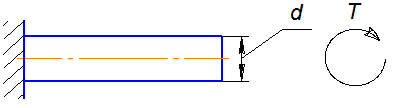
Рис. 4.19 Действие скручивающей нагрузки на вал
Решение. напряжение среза определяется по формуле:

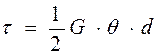 ,
,
где G – модуль упругости; q – угол закручивания на единицу длины; d – диаметр вала.
Крутящий момент 
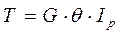 , где Ip – полярный момент инерции вала.
, где Ip – полярный момент инерции вала.
Для круглого вала сплошного сечения
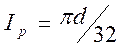 ;
; 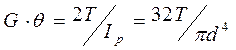 ;
; 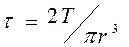 .
.
Применяя приближённые формулы расчёта, получают:
 =
= 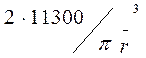 ;
;
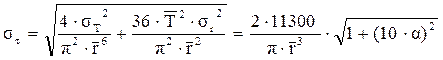 .
.
Для Rз = 0,999 из таблиц стандартного нормального распределения выбирается z = 3,09. Таким образом,
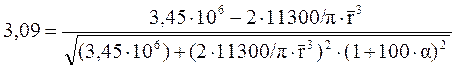 .
.
Выбирая a=0,03, получают: 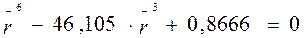 и окончательно для корней уравнения
и окончательно для корней уравнения 
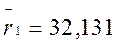 и
и 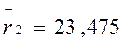 получают соответственно R = 0,999 и R = 0,001.
получают соответственно R = 0,999 и R = 0,001.
Влияние допуска a и прочности материала на надёжность R видно
из таблицы 4.8 и 4.9. В таблице 4.10 показано влияние радиуса вала на надёжность R.
Влияние допуска на надёжность
Таблица 4.8
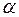 ,% ,%
| ||||
| Z | 3,099 | 3,072 | 3,035 | 2,772 |
| R | 0,99903 | 0,9969 | 0,9988 | 0,9974 |
Влияние прочности материала на надёжность
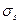 ,
МПа ,
МПа
| 34,475 | 41,37 | 55,166 | 68,95 |
| Z | 3,099 | 2,712 | 2,145 | 1,763 |
| R | 0,99903 | 0,9964 | 0,98422 | 0,96080 |
Таблица 4.9
|
Таблица 4.10
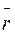 , мм , мм
| 30,48 | 32,131 | 35,56 | 40,64 |
| Z | 2,086 | 3,09 | 4,824 | 6,555 |
| R | 0,98169 | 0,999 | 0,9999 | 0,99999 |
5 Структурно-логический анализ технических
систем
5.1 Надёжность систем. Структурная схема надежности изделия
Оценка надёжности является одним из элементов сложной системы управления риском, предполагающей выполнение таких работ как идентификация и анализ риска, оценка пределов его допустимости и возможностей уменьшения путем выбора, осуществления и контроля управляющих действий.
Расчёт надежности технических систем производится с целью выбора лучших конструктивных решений, режимов эксплуатации, организации технического обслуживания и ремонта. Задачами надежности являются определение числовых показателей, выявление наиболее ненадежных элементов, определение наиболее эффективных мер повышения показателей надежности. Решение этих задач возможно после предварительного структурно - логического анализа системы.
Объект, как было ранее сказано, есть техническое изделие определенного целевого назначения, рассматриваемое в периоды проектирования, производства, испытаний и эксплуатации.
Большинство технических объектов представляют собой сложные системы, состоящие из отдельных деталей, узлов, агрегатов, устройств контроля, управления и т.д. Техническая система (ТС) – совокупность технических устройств (элементов), предназначенных для выполнения определенной функции или функций. Соответственно,элемент – составная часть системы.
Расчленение ТС на элементы достаточно условно и зависит от постановки задачи расчета надежности. Например, при анализе работоспособности технологической линии её элементами могут считаться отдельные установки и станки, транспортные и загрузочные устройства и т. д. В свою очередь станки и устройства также могут считаться техническими системами и при оценке их надежности должны быть разделены на элементы – комплексы, комплекты, сборочные единицы, детали, согласно классификации ЕСКД.
При определении структуры ТС в первую очередь необходимо оценить влияние каждого элемента и его работоспособности на работоспособность системы в целом. С этой точки зрения целесообразно разделить все элементы на четыре группы:
1. Элементы, состояние которых практически не влияет на работоспособность системы (например, деформация кожуха, изменение окраски поверхности и т. п.).
2. Элементы, работоспособность которых за время эксплуатации практически не изменяется и вероятность безотказной работы близка к единице (корпусные детали, малонагруженные элементы с большим запасом прочности).
3. Элементы, ремонт или регулировка которых возможна при работе изделия или во время планового технического обслуживания (наладка или замена технологического инструмента оборудования и т. д.).
4. Элементы, отказ которых сам по себе или в сочетании с отказами других элементов приводит к отказу системы.
Очевидно, при анализе надежности ТС целесообразно включать в рассмотрение только элементы последней группы.
Подход к объекту как к одному целому не позволяет выявить наиболее слабый элемент.
В новых конструкциях используется старый элемент, надёжность которого нам известна.
Не всякое изделие можно поставить на испытание в достаточном количестве экземпляров.
Для составления структурной схемы изделие разбивают на элементы, а затем рассматривают влияние отказа произвольно взятого элемента на надёжность всего объекта.
Вводятся уточнения:
· Если отказ элемента приводит к отказу всего объекта, то элемент считается встроенным в структурную схему последовательно.
· Если отказ элемента не приводит к отказу всего объекта, то элемент считается встроенным в структурную схему параллельно.
При составлении структурной схемы придерживаются следующих правил:
· Элементы изображаются в виде прямоугольников и обозначаются или номерами или индексами 1 (а).
· Одна сторона прямоугольника считается входом, другая – выходом для сигнала.
· Элемент считается работоспособным, если сигнал с входа элемента проходит на выход.
· Отказ элемента делает невозможным прохождение сигнала.
· Линии, соединяющие элементы друг с другом, считаются абсолютно безотказными.
Системы различаются:
· По принципу действия (механическая часть, электрическая часть, гидравлическая часть).
· По характеру выполняемых работ.
· По операциям, выполняемым машиной в течение цикла.
· Степень деления может быть разной. Для расчета и оценки критериев надежности подсистем достаточным будет их представление в виде отдельных сборочных элементов (корпус, вентилятор, воздуховод и т. п.).
Если же поставленная задача включает оптимизацию конструкции отдельных элементов, то деление должно быть более детальным и доходить до уровня отдельных узловых деталей.
Цель расчёта надёжности:
· обосновать выбор того или иного конструктивного решения;
· выяснить возможность и целесообразность резервирования;
· выяснить, достижима ли требуемая надежность при существующей технологии разработки и производства.
Анализ структурной надежности ТС, как правило, содержит следующие операции:
1. Рассматриваются выполняемые системой и её составными частями функции, а также взаимосвязь составных частей.
2. Формируется содержание понятия “безотказной работы” для данной конкретной системы.
3. Определяются возможные отказы составных частей и системы, их причины и возможные последствия.
4. Оценивается влияние отказов составных частей системы на ее работоспособность.
5. В системе выделяются элементы с известными показателями надежности.
6. Составляется структурно-логическая схема надёжности технической системы, которая является моделью её безотказной работы.
7. Составляются расчётные зависимости для определения показателей надёжности ТС с использованием данных по надёжности её элементов и с учётом структурной схемы.
8. В зависимости от поставленной задачи на основании результатов расчёта характеристик надёжности ТС делаются выводы и принимаются решения о необходимости изменения или доработки элементной базы, резервировании отдельных элементов или узлов, об установлении определённого режима профилактического обслуживания, о номенклатуре и количестве запасных элементов для ремонта и т. д.
Для расчётов параметров надёжности удобно использовать структурно - логические схемы надёжности ТС, которые графически отображают взаимосвязь элементов и их влияние на работоспособность системы в целом. Структурно-логическая схема представляет собой совокупность ранее выделенных элементов, соединенных друг с другом последовательно или параллельно. Критерием для определения вида соединения элементов (последовательного илипараллельного) при построении схемы является влияние их отказа на работоспособность ТС.
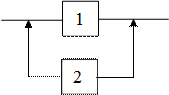
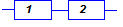
Последовательным (с точки зрения надёжности) считается соединение, при котором отказ любого элемента приводит к отказу всей системы (рис. 5.1).
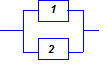
Параллельным (с точки зрения надежности) считается соединение, при котором отказ любого элемента не приводит к отказу системы, пока не откажут все соединенные элементы (рис. 5.2).


Рис. 5.1 Последовательное соединение элементов
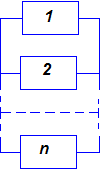
Рис. 5.2 Параллельное соединение элементов
Определенная аналогия здесь прослеживается с электрической цепью, составленной из проводящих элементов (исправный элемент пропускает ток, отказавший – не пропускает): работоспособному состоянию ТС соответствует возможность протекания тока от входа до выхода цепи.
Наиболее наглядным примером последовательных систем могут служить автоматические станочные линии без резервных цепей и накопителей. В них название реализуется буквально. Однако понятие "последовательная система" в задачах надежности шире, чем в задачах электротехники. К последовательным системам относятся все системы, в которых отказ элементов приводит к отказу всей системы. Примером параллельных систем являются электрические системы из электрических машин, работающих на общую сеть, многомоторные самолеты, суда с двумя машинами и резервные системы.
Однако не всегда структурная схема надежности аналогична конструктивной или электрической схеме расположения элементов. Например, подшипники на валу редуктора работают конструктивно параллельно друг с другом, однако выход из строя любого из них приводит к отказу системы. Эти элементы с точки зрения надежности образуют последовательное соединение.
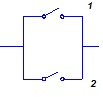
Кроме того, на структуру схемы надёжности может оказывать влияние и вид возникающих отказов. Например, в электрических системах для повышения надежности в ряде случаев применяют параллельное или последовательное соединение коммутирующих элементов (рис. 5.3). Отказ таких изделий может происходить по двум причинам: обрыв (то есть невозможность замыкания цепи) и замыкание (то есть невозможность разрыва соединения). В случае отказа типа “обрыв” схема надежности соответствует электрической схеме системы (“обрыв” в любом коммутаторе при последовательном соединении элементов приводит к отказу, при параллельном соединении все функции управления выполняет исправный коммутатор). В случае отказа типа “замыкание” схема надёжности противоположна электрической (при параллельном соединении утратится возможность отключения тока, а при последовательном соединении общего отказа не происходит).
| Электрическая схема | Структурная схема надёжности при отказе типа | |
| обрыв | замыкание | |
| 
|  
|
|

| 
|
Рис. 5.3 Электрические и структурные схемы соединения коммутационных элементов
при различных видах отказов
Контрольные вопросы:
1 Каковы основные цели и задачи расчета показателей надежности систем?
2 Перечислите и поясните основные этапы расчета надежности систем.
3 Что такое структурная схема надежности?
4 Назовите правила составления структурной схемы.
5 Как производится разбивка элементов по системам?
6 Зачем используется структурная схема безотказности изделия?
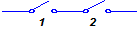
5.2 Расчёт надёжности последовательных систем
X Y

P 1(t) P 2(t) Pi (t) Pn (t)
X Y

P 1(t) P 2(t) Pi (t) Pn (t)
Рис. 5.4 Расчётная схема последовательного соединения элементов
Работоспособность такой системы обеспечивается при условии, когда все n элементов системы находятся в работоспособном состоянии.
Безотказность работы i – го элемента зависит от безотказности других:
Рс (t) = Р1 (t) · Р2 (t) · … · Рi (t) · … · Рn (t) = 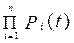 ; (5.1)
; (5.1)
Qс(t)= 1 - Рс (t) = 1 - 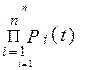 ; (5.2)
; (5.2)
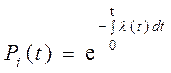 ;
;
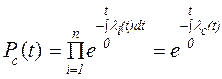 ; (5.3)
; (5.3)
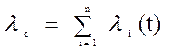 ; (5.4)
; (5.4)
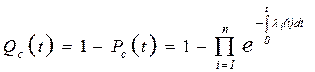 . (5.5)
. (5.5)
Если все элементы одинаковы, то:
1) при n = 30 Р1 = Р2 = … = Рi = … Рn;
Рс (t) = Р(t)n;
Р (t) = 0,99;
Рс (t) = 0,9930=0,7397.
2) при n = 500
Рс (t) = 0,0066.
Из (5.3) – (5.4) следует, что для системы из n элементовc одинаковой надежностью (λ = λ1) верно условие:
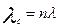 ; (5.6)
; (5.6)
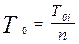 , (5.7)
, (5.7)
то есть интенсивность отказов в n раз больше, а средняя наработка в n раз меньше, чем у отдельного элемента.При последовательном соединении общая надёжность всей системы ниже надёжности самого слабого элемента. При очень большом количестве высоконадёжных элементов система может оказаться неработоспособной.
Повысить надёжность такой системы можно за счёт выполнения следующих действий:
· увеличения надёжности составных элементов;
· сокращения количества элементов;
· уменьшения интенсивности отказов (за счет уменьшения времени эксплуатации).
Контрольные вопросы и задачи
1 Что такое последовательная система и в чем состоит условие её безотказной работы?
2 Как рассчитывается вероятность безотказной работы последовательных систем?
3 Как можно повысить надёжность последовательных систем?
4 Как определяются показатели безотказности последовательной системы: вероятность безотказной работы и интенсивность отказов?
5 Какой закон распределения наработки до отказа будет иметь последовательная система, если законы распределения наработки до отказа элементов являются экспоненциальными?
6 Структура проектируемой системы представляется последовательной системой, состоящей из 10 элементов A, 15 элементов B, 32 элемента D и 8элементов F. Интенсивности отказов элементов известны и равны:
λA = 2 · 10 - 6 ч - 1, λB = 4 · 10 - 6 ч - 1, λD = 2.5 · 10 - 6 ч - 1, λF = 5 · 10 - 6 ч - 1.
Определить среднюю наработку до отказа T0с и ВБР системы при наработках
t1 = 100 ч, t2 = 1000 ч.

Ответ: T0 с = 5 · 10 3 ч, P (t1 ) = 0,98, P (t2 ) = 0,819.
5.3 Расчёт надёжности параллельных систем
Рис. 5.5 Расчетная схема параллельного соединения элементов
Отказ системы произойдёт при отказе всех элементов.
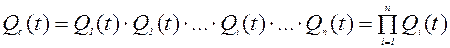 , (5.8)
, (5.8)
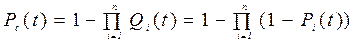 , (5.9)
, (5.9)
Например, при Pi (t) = 0,86, n = 3 Pc (t) = 1 – (1 – 0,86)3 = 0,997.
При параллельном соединении можно сформировать надёжную конструкцию из самых ненадёжных элементов:
(P (t) + Q(t)) m = 1,
где m – количество элементов.
Например, при m = 2 (P (t) +Q(t)) m = P2+2PQ+Q2 = 1,
здесь P 2 означает вероятность безотказной работы обоих элементов;
2× PQ – вероятность отказа одного элемента, при этом второй элемент останется работоспособным;
P 2+2 PQ – из строя выйдет (откажет) не более одного элемента; Q 2 – вероятность отказа обоих элементов;
P = Q = 0,5; 0,25 + 0,5 + 0,25 = 1;
при m = 3 (P (t) +Q (t)) m = Р 3 + 3 Р 2 Q+ 3 РQ 2 +Q 3 = 1;
Р 3 – все три элемента работоспособны; 3 Р 2 Q – из строя выйдет не более одного элемента;
3 QP 2 – из строя выйдет не более двух элементов;
Q 3 – из строя выйдут все три элемента.
Из приведенного примера видно, что надёжность системы с параллельным соединением повышается при увеличении числа элементов.
При экспоненциальном распределении наработки выражение (5.9) принимает вид:
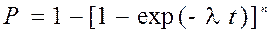 , (5.10)
, (5.10)
откуда после интегрирования и преобразований средняя наработка системы определяется:
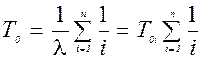 , (5.11)
, (5.11)
где 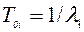 − средняя наработка элемента. При больших значениях n справедлива приближенная формула:
− средняя наработка элемента. При больших значениях n справедлива приближенная формула:
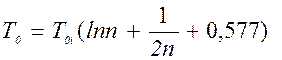 . (5.12)
. (5.12)
Таким образом, средняя наработка системы с параллельным соединением больше средней наработки её элементов (например, при 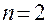
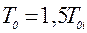 , при n =3
, при n =3 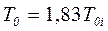 ).
).
Контрольные вопросы:
1 Что такое последовательная система, каковы условия её безотказной работы?
2 Что такое параллельная система, каковы условия ее безотказной работы?
3 Как рассчитывается вероятность безотказной работы параллельных систем?
4 Как можно повысить надёжность параллельных систем?
5 Как определяются показатели безотказности параллельной системы: вероятность безотказной работы и средняя наработка системы?
Date: 2015-07-17; view: 3187; Нарушение авторских прав