Перевірка гіпотез про рівність математичних сподівань та дисперсій для нормальних сукупностей.

Нехай ξ та h — дві незалежні випадкові величини, кожна з яких має нормальний розподіл та У результаті спостережень цих випадкових величин отримано дві вибірки z=(ξ ₁, ξ ₂, …, ξ_{n 1}) та γ =(h ₁, h ₂, …, h_{n 2}). 1.Гіпотеза про рівність математичних сподівань при відомих дисперсіях. Необхідно перевірити гіпотезу проти альтернативної гіпотези та — відомі. Критична множина задається нерівністю:

— реалізація вибірок z та γ,

α — похибка першого роду, тобто ймовірність прийняти гіпотезу H ₁, коли правильна H ₀, 2 Ф (C _a)=1– a..Якщо (X, Y) R_{n 1}, то приймається гіпотеза H ₁, якщо ж (X, Y)Ï R_{n 1}, то приймається H ₀.

2.Гіпотеза про рівність математичних сподівань при невідомих дисперсіях. Нехай потрібно перевірити такі ж гіпотези, як і в попередньому випадку, але і величина невідома. Критична множина задається нерівністю:

де

Число знаходиться за таблицею Стьюдента (таблиця 6 додатка) при числі степенів свободи і

3.Гіпотеза про рівність дисперсій при невідомих математичних сподіваннях. Нехай тепер потрібно перевірити гіпотезу проти альтернативної гіпотези При справедливості гіпотези H ₀ випадкова величина має розподіл Фішера—Снедекора з степенями свободи. Тоді критична множина задається нерівністю:

де 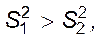чого завжди можна досягти, змінивши індекси, 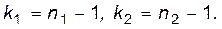Величина знаходиться за таблицею розподілу Фішера—Снедекора (таблиця 7 додатка).

4.Гіпотеза про рівність дисперсій при відомих математичних сподіваннях. Ця гіпотеза перевіряється аналогічно попередній, але в даному випадку ,де Якщо правильна гіпотеза 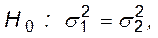то випадкова величина F має розподіл Фішера—Снедекора з степенями свободи. Критична множина задається нерівністю:

40.Лінійна регресія.

Регресія. Нехай ξ та h — дві випадкові величини (залежні у загальному випадку), і ми хочемо знайти найкраще в деякому розумінні наближення величини h деякою функцією g (ξ) від величини . Величина g (x) називається найліпшим наближенням величини h в середньому квадратичному, якщо

Лінійна регресія. Розглянемо регресію в класі лінійних функцій, тобто припустимо, що

де  і  — невідомі параметри.

Введемо такі позначення:

тобто —коефіцієнт кореляції.

Лінійна середньоквадратична регресія величини h на величину  має вигляд:

Повернемося тепер до сформульованої на початку задачі про найліпше визначення функції 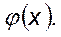Будемо вважати, що функція належить деякій параметричній сукупності функцій і ми маємо спостереження

Означення. Оцінкою невідомих параметрів за методом найменших квадратів буде вектор , при якому досягається мінімум функції:

а функція буде найліпшим середньоквадратичним наближенням, що відновлює залежність між x та y за результатами наших спостережень.

Розглянемо важливий випадок, коли функція має вигляд

де k і b — невідомі параметри. У цьому випадку оцінками параметрів лінійної регресії будуть числа та , при яких функція досягає мінімуму.Тоді

де

У випадку поліноміальної регресії

оцінки невідомих параметрів знаходяться з системи лінійних алгебраїчних рівнянь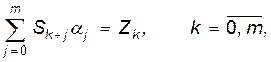

де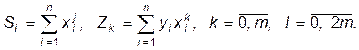

Якщо значення відомі без похибок, а значення незалежні та рівноточні, то оцінка дисперсії (похибка вимірювань) величини визначається за формулою:

де

Оцінки дисперсій коефіцієнтів визначаються за формулами:

де 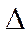— визначник системи, а — алгебраїчне доповнення до елемента, який стоїть на діагоналі й має індекс k у визначнику У випадку лінійної регресії

Якщо величини мають нормальний розподіл, то для коефіцієнтів справеджуються такі надійні інтервали:

де — оцінки, отримані методом найменших квадратів, а число знаходиться за таблицею розподілу Стьюдента (таблиця 6 додатка) при числі степенів свободи і

Вибірковий коефіцієнт кореляції визначається за формулою:

Коефіцієнт кореляції рангів. У деяких випадках натрапляємо на ознаки, які не піддаються кількісним оцінкам. Тоді кожній оцінці можна поставити у відповідність порядковий номер, який назвемо рангом. Нехай n осіб за якістю A мають ранги а за якістю B — , де всі X та Y є перестановками n перших чисел натурального ряду. — різниця рангів.Тоді коефіцієнт кореляції рангів Спірмена, або коефіцієнт щільності зв’язку між A та B, визначається за формулою:

Є й і інші показники щільності зв’язку між рангами. Якщо не можна визначити рангову відмінність декількох осіб, то беруть середній ранг. У цьому випадку використовують коефіцієнт кореляції рангів Кендела:

де 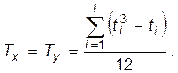— число об’єднаних рангів для X та Y.

1.Формули комбінаторики. 1

2.Випадкова подія. Операції над подіями. 4

3.Класичне означення ймовірності 5

4.Геометрична ймовірність. 6

5.Аксіоми теорії ймовірності 7

6.Властивості ймовірності 8

7.Умовна ймовірність.Незалежність подій. 9

8. Формула повної ймовірності. Формула Байєса. 10

9.Послідовність незалежних випробувань.Схема Бернуллі. 11

10.Найімовірніше число випробувань в схемі Бернуллі. 12

11. Локальна теорема Муавра-Лапласа: 14

12. Інтегральна теорема Муавра-Лапласа: 15

13.Теорема Пуассона. 16

14. Функції розподілу випадкових величин. Властивості. 17

15.Дискретні випадкові величини. 18

16. Математичне сподівання випадкової величини. Властивості математичного сподівання. 19

17. Дисперсія випадкової величини. Властивості дисперсії 20

18.Основні дискретні розподіли та їхні числові характеристики 21

19.Неперервні випадкові величини. 24

20. Щільність ро зподілу Неперервні випадкові величини 25

21. Математичне сподівання неперервної випадкової величини. 26

22. Дисперсія неперервної випадкової величини. 27

23.Основні неперервні розподіли та їх числові хар-ки. 28

24.Нормальний розподіл в.в.Правило 3-х сигм. 30

25.Розподіл функції випадкової величини. 31

26.Сумісний розподіл випадкових величин. 33

27.Коваріація. Коефіцієнт кореляції двох випадкових величин 34

28.Нерівності Маркова і Чебишева. 35

29.Вибірка з генеральної сукупності. Статистичний та інтервальний статистичний ряд. 37

Частота. 38

30.Статистична функція розподілу. Гістограма. 39

31.Точкові оцінки для математичного сподівання та дисперсії 41

32.Методи моментів і максимальної правдоподібності побудови статистичних оцінок параметрів. 45

33. Надійні інтервали. 47

34. Побудова надійних інтервалів для математичного сподівання і дисперсії нормального закону. 48

35.Cтатистична гіпотеза та загальна схема її перевірки. 49

36. Перевірка гіпотез про вигляд розподілу(критерій Колмогорова та критерій про вигляд розподілу. 51

37.Критерії однорідності (критерій Смирнова – Колмогорова та критерій однорідності ) Критер.Смирн-Колмог. 54

38. Перевірка гіпотез про незалежність (критерій незалежності ) 56

39.Перевірка гіпотез про рівність математичних сподівань та дисперсій для нормальних сукупностей. 57

40.Лінійна регресія. 60

Date: 2016-08-31; view: 604; Нарушение авторских прав