Статистична функція розподілу. Гістограма

Випадковою вибіркою об’єму n (чи вибіркою) називається випадковий вектор ξ ₁, ξ ₂, …, ξ_n, де ξ_i — незалежні і однаково розподілені Іноді кажуть, що вибірка ξ ₁, ξ ₂, …, ξ_n добута з генеральної сукупності випадкової величини ξ з функцією розподілу Fξ (x). Реалізацію вибірки будемо позначати відповідно X= (x ₁, x ₂, …, x_n).

Розташуємо величини x ₁, x ₂, …,x_n у порядку зростання: x ₍₁₎ ≤ x ₍₂₎ ≤ …≤ x _(n), де друга за величиною серед 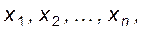Позначимо через ξ _(k) випадкову величину, яка для кожної реалізації X вибірки ξ набуває значення x _(k), k= 1,2, …,n. Отримали нову послідовність випадкових величин ξ ₍₁₎, ξ ₍₂₎, …, ξ _(n), які називаються порядковими статистиками. Причому вони задовольняють нерівність:

Ця послідовність називається варіаційним рядом вибірки.

Позначимо через n _n (x) випадкову величину, рівну числу елементів вибірки z ξ ₁, ξ ₂, …, ξ_n), значення яких менші x, і позначимо, 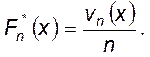Функція називається емпіричною функцією розподілу. Її можна використовувати як оцінку функції Легко бачити, що — випадкова величина, яка набуває значення {1; 2; …; 1} з імовірністю:

Для кожної реалізації X вибірки z функція задовольняє всі властивості функції розподілу: змінюється від 0 до 1, неперервна зліва, неспадна.

Якщо всі компоненти вектора X різні, то

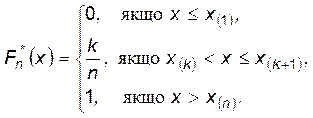
Нехай тепер ξ неперервна випадкова величина з щільністю p (x). Для оцінки p (x) з реалізації X= (x ₁, x ₂, …, x_n) вибірки ξ розіб’ємо множину значень ξ на s інтервалів довжини h_i, i= 1, 2, …, s. Нехай – середина i -го інтервалу, – кількість елементів x_j, j= 1, 2, …, n, які потрапили в i -ий інтервал. Тоді – оцінка щільності в точці . Прямокутники з основами h_і і висотами , i= 1, 2, …, s у прямокутній системі координат називаються гістограмою вибірки. Якщо на гістограмі ординати відповідні послідовно з’єднати відрізками прямих, то здобута ламана буде полігоном частот. Полігон частот є також статистичним аналогом теоретичної щільності. Для інтервальних оцінок .

Date: 2016-08-31; view: 293; Нарушение авторских прав