Методи моментів і максимальної правдоподібності побудови статистичних оцінок параметрів

Нехай z=(ξ ₁, ξ ₂, …, ξ_n) — вибірка з генеральної сукупності з розподілом де q =(q ₁, q ₂, …, q_s), Припустимо, що у випадковій величині ξ, що спостерігається, є перші s моментів При цьому вони є функціями від невідомих параметрів q: 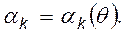Нехай — реалізація вибірки z. Значення оцінок параметрів за методом моментів знаходиться в результаті розв’язку системи рівнянь:

Оцінки, знайдені методом моментів, як правило, спроможні, але часто неефективні.

Нехай спостерігається випадковий вектор z=(ξ ₁, ξ ₂, …, ξ_n) з щільністю і 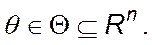Оцінкою максимальної правдоподібності називається така точка множини 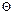, в якій функція правдоподібності при заданому X набуває максимального значення. Тобто

У багатьох випадках знаходять причому максимум досягається в тих же точках, що і

Якщо для кожного X з вибіркового простору Rⁿ максимум досягається у внутрішній точці і функція диференційована за , то оцінка при заданій реалізації 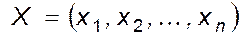вектора z задовольняє систему рівнянь:

або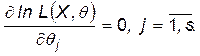

Останні рівняння називаються рівняннями правдоподібності.

Якщо для параметра q існує достатня статистика T (X), то розв’язок рівнянь правдоподібності є функцією від достатньої статистики.

Нехай q — скалярний параметр. Якщо для параметра q існує ефективна незміщена оцінка, то вона збігається з оцінкою максимальної правдоподібності.

Надійні інтервали.

Нехай z — вибірковий вектор об'єму n, — розподіл вектора z, який залежить від невідомого параметра q. При інтервальному оцінюванні невідомого параметра q шукають такі дві статистики і в яких і для яких при заданому виконується умова: Тоді інтервал називається (1–α-надійним інтервалом, імовірність 1– α — рівнем надійності, а і — нижньою та верхньою межами надійності. Інтервал — асимптотично найкоротший (1– α - надійний інтервал.

Date: 2016-08-31; view: 296; Нарушение авторских прав