Действия над матрицами

1. Умножение матрицы на число
Произведением матрицы 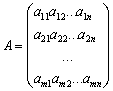на число λ называется матрица .
Пример. Найти произведение матрицы на число λ=3.

.

2.Сложение (вычитание) матриц
Суммой (разностью) матриц А и В, в каждой из которых m строк и n столбцов, называется матрица С с элементами, равными суммам (разностям) соответствующих элементов слагаемых:


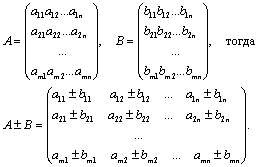
Пример. Найти сумму матриц и .

Решение. .

3.Умножение матриц
Пусть даны матрица 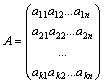размерности и
матрица 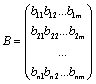размерности .
Пусть число столбцов матрицы А совпадает с числом строк матрицы В (в этом случае матрицу А называют согласованной с матрицей В).
Произведением матрицы А на матрицу В называется такая матрица размерности , каждый элемент которой находится как сумма произведений элементов, взятых по порядку из i -й строки матрицы А и j -го столбца матрицы В.
Пример. Найти произведение матриц и .
Решение: .
Пример. Найти произведение матриц
Решение: .
Еще раз отметим, что в матрице-произведении число строк равно числу строк матрицы А и число столбцов равно числу столбцов матрицы В.

Определители

Понятие определителя вводится только для квадратной матрицы и представляет собой число, которое находится по определенному правилу через элементы, составляющие данную матрицу.
Для квадратной матрицы 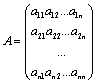n -го порядка определитель n -го порядка обозначается символом:
Δ= .(1)
В определителе различают строки и столбцы. Числа a_ij (i =1,…, n; j =1,…, n) называются элементами определителя.
Определение. Минором М_ij элемента а_ij определителя (1) называется определитель (n -1)-го порядка, который получается из определителя Δ путем вычеркивания i -ой строки из j -го столбца, на пересечении которых стоит элемент а_ij.
Определение. Алгебраическим дополнением А _ij элемента а_ij называетсяпроизведение (-1) ^{i + j} М_ij.
Не вводя строгое понятие определителя, дадим лишь правило его нахождения.
Определитель Δ = n -го порядка находится по формуле:
Δ (2)

где i - любое из чисел 1,2,…, n, А _ij – алгебраическое дополнение элемента а _ij.
Найдем по формуле (2) определитель 2-го порядка, выбрав, например, i =1: Δ = .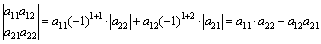
Из формулы (2) следует, что вычисление определителей >N -го порядка сводится к вычислению определителей (>n -1)-го порядка (т.е. миноров). Те, в свою очередь, опять по формуле (2) сводятся к определителям (n -2)-го порядка. Процесс нахождения определителей продолжается до получения миноров 2-го или 1-го порядка. Запись (2) называется разложением определителя по элементам i -ой строки.
Пример. Вычислить определитель третьего порядка Δ = .
Решение: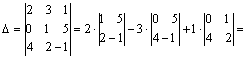
.
Разложение было выполнено по элементам 1-ой строки.
Заметим, что если некоторые элементы строки, по элементам которой производится разложение, равны нулю, то вычисление значительно упрощается. Обычно, пользуясь свойствами определителя, преобразуем его таким образом, чтобы в выбранной строке (выбранном столбце) все элементы кроме одного, равнялись нулю.

Date: 2016-08-30; view: 371; Нарушение авторских прав