Уравнения линий и поверхностей в пространстве.

Уравнение поверхности в пространстве содержит 3 переменные:

G(x, y, z)=0.

Вместо прямоугольных декартовых координат можно использовать любые другие. Вместо уравнений можно рассматривать неравенства. Цилиндрическая поверхность с образующей, параллельной оси Oz, описывается урав­

нением вида

G(x, y)=0.

Это же уравнение является одновременно уравнением направляющей.

Параметрические уравнения линий и поверхностей в пространстве.

Ззадание линий в пространстве:

x = ϕ(t),y = ψ(t),z = χ(t),α t β.

С точки зрения механики параметрические уравнения линии — это закон движения материальной точки, параметр t — время.

Пример.

Винтовая линия. Точка совершает два одновременных движения: равномерное враще­ние с угловой скоростью ω в плоскости Oxy по окружности радиуса R и равномерное поступательное движение вдоль оси Oz со скоростью c:

x = R cos ωt, y = R sin ωt, z = ct.

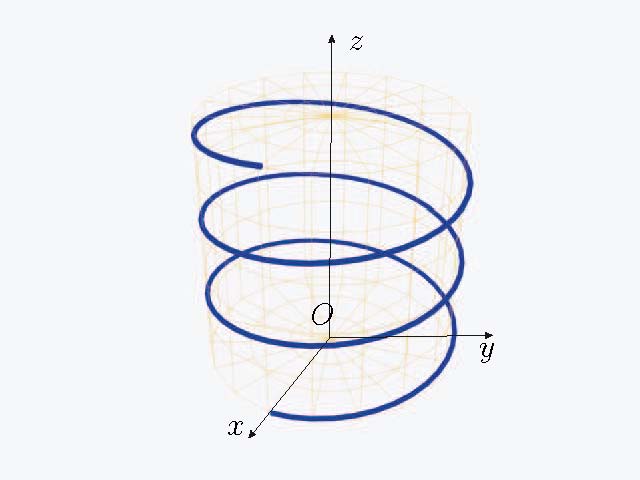
Пример.

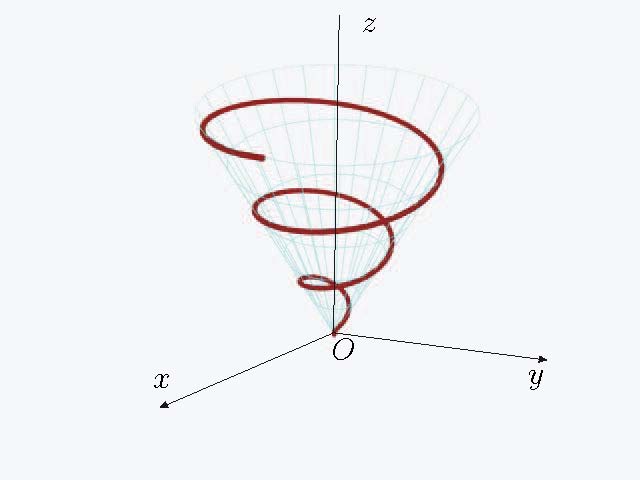
Коническая винтовая линия.

x = t cos t, y = t sin t, z = t.

Параметрическое задание поверхностей. Поверхности задаются:

(1) уравнениями вида F (x, y, z)=0;

(2) параметрическими уравнениями вида

x = ϕ(u, v), y = ψ(u, v), z = χ(u, v), (u, v) ∈ D ⊂ R²;

параметры u, v — внутренние координаты поверхности;

(3) как графики функции двух переменных: z = f(x, y).

Пример.

Сфера радиуса R с центром в начале координат:

x²+y²+z²= R²

Параметрическое представление:

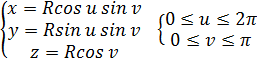
Представить сферу как график функции невозможно, но это удается сделать отдельно для нижней и верхней полусфер:

ЛЕКЦИЯ 3

. Тема: Матричная алгебра

Матрицы и определители, их свойства и действия над ними

При решении Биологических задач применяются методы математического моделирования, использующие решение систем линейных алгебраических уравнений. Для изучения методов решения систем уравнений введем понятия матриц и определителей.

Виды матриц

Определение. Таблица m x n чисел a_ij вида
, состоящая из m строк и n столбцов, называется матрицей.
Числа a_ij, стоящие на пересечении i -й строки и j -го столбца, называются элементами матрицы.
Матрицы А=(а_ij) и В=(b_ij) называются равными, если они имеют одинаковые размеры и для каждой пары индексов выполняется равенство a_ij = b_ij.
Нулевой матрицей называется матрица, все элементы которой равны нулю:
.
Матрица, у которой m=n, называется квадратной матрицей n -го порядка.
В квадратной матрице элементы a ₁₁, а ₂₂, … а_nn составляют главную диагональ. Квадратная матрица, у которой каждый элемент главной диагонали равен единице, а все остальные элементы равны нулю, называется единичной:
.

Date: 2016-08-30; view: 592; Нарушение авторских прав