
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Свойства определителей
|
|
Величина определителя не меняется от замены строк столбцами (проверьте самостоятельно). Из этого свойстваследует, что определитель можно найти, разлагая его также и по элементам какого-либо столбца: Δ =  , где j - номер любого из столбцов.
, где j - номер любого из столбцов.
Если любую строку или столбец матрицы умножить на некоторое число, то определитель также умножится на это число. При этом общий множительэлементов любой строки (столбца) можно вынести за знак определителя.
Величина определителя не изменится, если к элементам любой строки (столбца) прибавить элементы любой другой строки (столбца), умноженные на произвольное одинаковое число.
Пример: Вычислить определитель четвертого порядка:
Δ =  .
.
Решение.
1) Вынесем из второго столбца за знак определителя общий множитель 2; умножим первую строку на (–4) и сложим со второй строкой; умножим первую строку на (–3) и сложим с третьей; умножим первую строку на (–2) и сложим с четвертой, получим:
Δ = 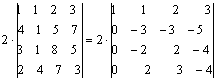 .
.
Вынесем за знак определителя из третьей строки общий множитель 2, получим определитель
Δ =  .
.
Разложим определитель Δ по элементам первого столбца, получим определитель третьего порядка, который вычислим, разлагая его по элементам 1-й строки:

Обратная матрица
Определение. Квадратная матрица n -го порядка называется невырожденной, если ее определитель n -го порядка Δ 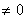 . Если определитель матрицы равен нулю, то она называется вырожденной.
. Если определитель матрицы равен нулю, то она называется вырожденной.
Определение. Матрица В называется обратной для данной квадратной матрицы А, если АВ = ВА = Е, где Е – единичная матрица. Обратную матрицу для данной матрицы А обозначают А -1, поэтому:
А -1= А -1 А = Е.
Если квадратная матрица невырожденная, то для нее существует единственная обратная матрица.
Пусть задана квадратная матрица
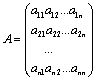 .
.
Тогда обратная матрица А -1 находится следующим образом:
 ,
,
где Δ – определитель матрицы А, Аij – алгебраическое дополнение элемента а ij (i =1,…, n; j =1, …, n). Необходимо обратить внимание, что, находя алгебраические дополнения к элементам строк матрицы А, в обратной матрице А -1 мы записываем их по соответствующим столбцам.
Пример. Найти матрицу, обратную матрице 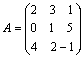 .
.
Проверить результат, вычислив произведение данной и обратной матриц.
Решение. Определитель матрицы А вычислен ранее:
Δ = 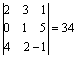 .
.
Так, как Δ 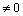 , то матрица А невырожденная и для нее существует обратная.
, то матрица А невырожденная и для нее существует обратная.
Найдем алгебраические дополнения каждого элемента матрицы А:

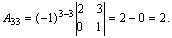
Следовательно: 
Проверка: 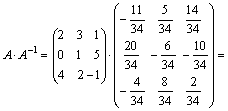
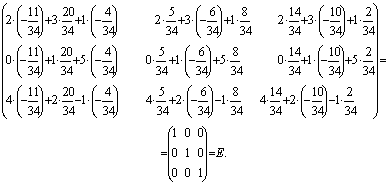
Ответ:  .
.
.
ЛЕКЦИЯ 4
Тема: Решение систем линейных уравнений.
Свойства определителей. Обратные матрицы. Методы решения си стем линейных уравнений.
Определитель единичной матрицы равен 1.
Обратная матрица
Определение. Квадратная матрица n -го порядка называется невырожденной, если ее определитель n -го порядка Δ 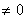 . Если определитель матрицы равен нулю, то она называется вырожденной.
. Если определитель матрицы равен нулю, то она называется вырожденной.
Определение. Матрица В называется обратной для данной квадратной матрицы А, если АВ = ВА = Е, где Е – единичная матрица. Обратную матрицу для данной матрицы А обозначают А -1, поэтому:
А -1= А -1 А = Е.
Если квадратная матрица невырожденная, то для нее существует единственная обратная матрица.
Пусть задана квадратная матрица
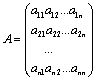 .
.
Тогда обратная матрица А -1 находится следующим образом:
 ,
,
где Δ – определитель матрицы А, Аij – алгебраическое дополнение элемента а ij (i =1,…, n; j =1, …, n). Необходимо обратить внимание, что, находя алгебраические дополнения к элементам строк матрицы А, в обратной матрице А -1 мы записываем их по соответствующим столбцам.
Пример. Найти матрицу, обратную матрице 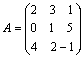 .
.
Проверить результат, вычислив произведение данной и обратной матриц.
Решение. Определитель матрицы А вычислен ранее:
Δ = 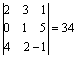 .
.
Так, как Δ 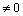 , то матрица А невырожденная и для нее существует обратная.
, то матрица А невырожденная и для нее существует обратная.
Найдем алгебраические дополнения каждого элемента матрицы А:

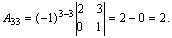
Следовательно: 
Проверка: 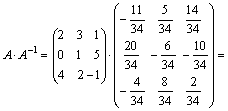
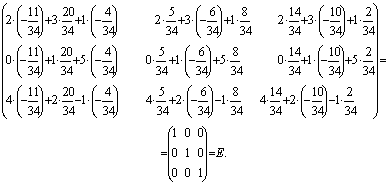
Ответ:  .
.
Свойство1. Важным свойством определителей является следующее соотношение:
det A = det AT;
Свойство 2. det (AB) = detA×detB
Свойство 3. Если в квадратной матрице поменять местами какие-либо две строки (или столбца), то определитель матрицы изменит знак, не изменившись по абсолютной величине.
Свойство 4. При умножении столбца (или строки) матрицы на число ее определитель умножается на это число.
Определение: Столбцы (строки) матрицы называются линейно зависимыми, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.
Свойство 6. Если в матрице А строки или столбцы линейно зависимы, то ее определитель равен нулю.
Свойство 7. Если матрица содержит нулевой столбец или нулевую строку, то ее определитель равен нулю. (Данное утверждение очевидно, т.к. считать определитель можно именно по нулевой строке или столбцу.)
Свойство 8. Определитель матрицы не изменится, если к элементам одной из его строк(столбца) прибавить(вычесть) элементы другой строки(столбца), умноженные на какое-либо число, не равное нулю.
Свойство 9. Если для элементов какой- либо строки или столбца матрицы верно соотношение: d = d1 ± d2, e = e1 ± e2, f = f1 ± f2, то верно:

Решение систем линейных уравнений
Метод Крамера.
(Габриель Крамер (1704-1752) швейцарский математик)
Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных.
Для этого необходимо, чтобы определитель матрицы системы не равнялся 0.
det A ¹ 0;
Действительно, если какое- либо уравнение системы есть линейная комбинация остальных, то если к элементам какой- либо строки прибавить элементы другой, умноженные на какое- либо число, с помощью линейных преобразований можно получить нулевую строку. Определитель в этом случае будет равен нулю.
Теорема. (Правило Крамера):
Теорема. Система из n уравнений с n неизвестными
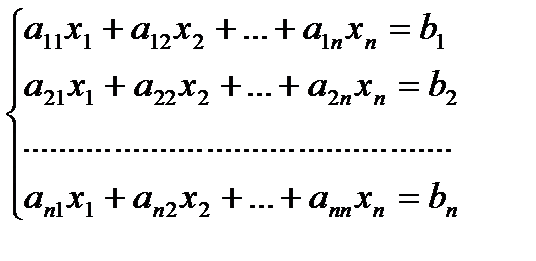
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi = Di/D, где
D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Di = 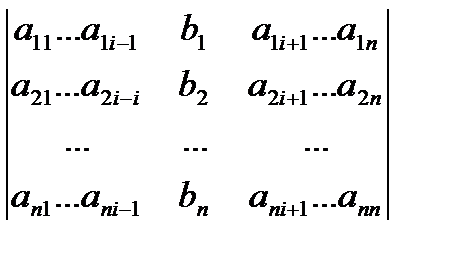
Пример.
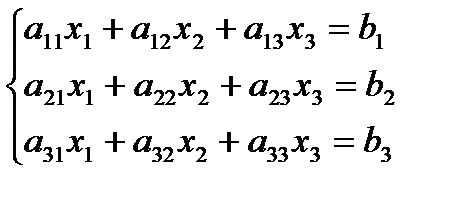
A =  ; D1=
; D1= 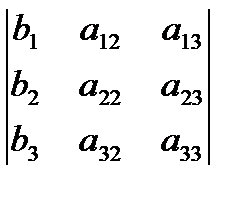 ; D2=
; D2=  ; D3=
; D3= 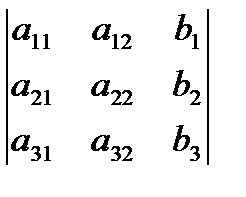 ;
;
x1 = D1/detA; x2 = D2/detA; x3 = D3/detA;
Пример. Найти решение системы уравнений:
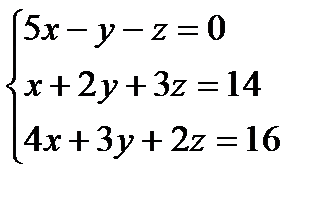
D = 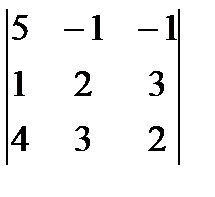 = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
D1 = 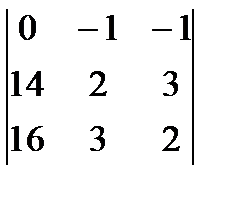 = (28 – 48) – (42 – 32) = -20 – 10 = -30.
= (28 – 48) – (42 – 32) = -20 – 10 = -30.
x1 = D1/D = 1;
D2 = 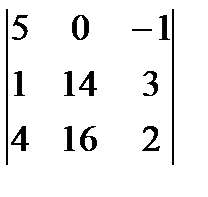 = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
x2 = D2/D = 2;
D3 = 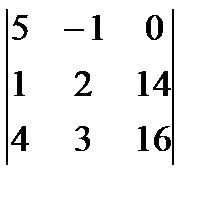 = 5(32 – 42) + (16 – 56) = -50 – 40 = -90.
= 5(32 – 42) + (16 – 56) = -50 – 40 = -90.
x3 = D3/D = 3.
Если система однородна, т.е. bi = 0, то при D¹0 система имеет единственное нулевое решение x1 = x2 = … = xn = 0.
При D = 0 система имеет бесконечное множество решений.
Для самостоятельного решения:
 ; Ответ: x = 0; y = 0; z = -2.
; Ответ: x = 0; y = 0; z = -2.
Date: 2016-08-30; view: 429; Нарушение авторских прав