Угол между прямой и плоскостью

Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями

Рассмотрим векторы и . Если угол между ними острый, то он будет , где φ – угол между прямой и плоскостью. Тогда .

Если угол между векторами и тупой, то он равен . Следовательно . Поэтому в любом случае 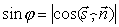. Вспомнив формулу вычисления косинуса угла между векторами, получим .

Условие перпендикулярности прямой и плоскости.

Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой и нормальный вектор плоскости коллинеарны, т.е. .

Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы и перпендикулярны.

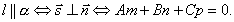
Примеры.

1. Написать уравнение плоскости, проходящей через точку М ₁(2;-3;4) параллельно прямым и .

Так как M₁  α, то уравнение плоскости будем искать в виде

.

Применяя условие параллельности прямой и плоскости, получим систему линейных уравнений

Отсюда

Итак, или .

1. Найти угол между прямой и плоскостью .

Направляющий вектор прямой . Нормальный вектор плоскости . Следовательно,

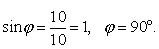
1. Найдите точку, симметричную данной М (0;-3;-2) относительно прямой .

Составим уравнение плоскости α перпендикулярной l. M  α, . Следовательно, или .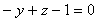

Найдём точку пересечения прямой l и α:

Итак, N (0.5;-0.5;0.5). Пусть искомая точка М ₁ имеет координаты М ₁(x,y,z). Тогда очевидно равенство векторов 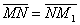, т.е. (0,5;2,5;2,5)=(х -0.5; у +0.5; z -0.5). Откуда x =1, y =2, z =3 или М ₁(1;2;3)..

Date: 2016-08-30; view: 374; Нарушение авторских прав