Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Общие уравнения прямой, как линии пересечения двух плоскостей
|
|
Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.
Вообще любые две не параллельные плоскости, заданные общими уравнениями
определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.
Примеры.
Построить прямую, заданную уравнениями 
Для построения прямой достаточно найти любые две ее точки. Проще всего выбрать точки пересечения прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений прямой, полагая z = 0:
Решив эту систему, найдем точку M 1(1;2;0).
Аналогично, полагая y = 0, получим точку пересечения прямой с плоскостью xOz:
От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти какую-либо точку М 1 на 
прямой и направляющий вектор 
прямой.
Координаты точки М 1 получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к обоим нормальным векторам 
и 
. Поэтому за направляющий вектор прямой l можно взять векторное произведение нормальных векторов:
.
Пример. Привести общие уравнения прямой 
к каноническому виду.
Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y = 0 и решим систему уравнений:
Нормальные векторы плоскостей, определяющих прямую имеют координаты 
Поэтому направляющий вектор прямой будет
. Следовательно, l: 
.
Угол между прямыми
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
Пусть в пространстве заданы две прямые:
Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами 
и 
. Так как 
, то по формуле для косинуса угла между векторами получим
.
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов 
и :
Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l 1 параллельна l 2 тогда и только тогда, когда 
параллелен 
.
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: 
.
Примеры.
- Найти угол между прямыми
и 
.
- Найти уравнения прямой проходящей через точку М 1(1;2;3) параллельно прямой l 1:
Поскольку искомая прямая l параллельна l 1, то в качестве направляющего вектора искомой прямой l можно взять направляющий вектор прямой l 1.
- Составить уравнения прямой, проходящей через точку М 1(-4;0;2) и перпендикулярной прямым:
и 
.
Направляющий вектор прямой l можно найти как векторное произведение векторов и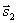 
:
Date: 2016-08-30; view: 538; Нарушение авторских прав