
Главная
Случайная страница
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
|
Общее уравнение плоскости
Можно показать, что любое уравнение первой степени относительно декартовых координат x, y, z представляет собой уравнение некоторой плоскости. Это уравнение записывается в виде:
Ax+By+Cz+D =0
и называется общим уравнением плоскости, причём координаты A, B, C здесь являются координатами нормального вектора плоскости.
Рассмотрим частные случаи общего уравнения. Выясним, как располагается плоскость относительно системы координат, если один или несколько коэффициентов уравнения обращаются в ноль.
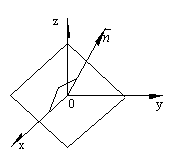 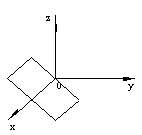 
| - Свободный член равен нулю D = 0.
В этом случае уравнение плоскости принимает вид Ax+Cy+Bz =0. Т.к. числа x =0, y =0, z =0 удовлетворяют уравнению плоскости, то она проходит через начало координат.
- Один из коэффициентов при текущих координатах равен нулю. Пусть например A =0. В этом случае уравнение плоскости имеет вид By+Cz+D =0. Нормальный вектор плоскости имеет координаты
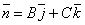 и перпендикулярен оси Ox. Следовательно, плоскость параллельна оси Ox. и перпендикулярен оси Ox. Следовательно, плоскость параллельна оси Ox. Аналогично, если B = 0, то плоскость параллельна оси Oy и C = 0 – плоскость параллельна оси Oz.
Т.о., если в уравнении плоскости один из коэффициентов при текущей координате равен нулю, то плоскость параллельна соответствующей координатной оси.
- Коэффициент при текущей координате и свободный член равны нулю. Например, A = D = 0. В этом случае уравнению By + Cz = 0 соответствует плоскость, проходящая через начало координат (согласно п.1). Кроме того, учитывая п.2, данная плоскость должна быть параллельна оси Ox. Следовательно, плоскость проходит через ось Ox.
Аналогично, при B=D =0 плоскость Ax+Cz =0 проходит через ось Oy. При C=D =0 плоскость проходит через ось Oz.
- Два коэффициента при текущих координатах раны нулю. Пусть, например, A=B =0. Тогда плоскость Cz+D =0 в силу п.2 будет параллельна осям Ox и Oy, а следовательно параллельна координатной плоскости xOy, и проходит через точку с координатой. Аналогично, уравнениям Ax+D =0 и By+D =0 соответствуют плоскости, параллельные координатным плоскостям yOz и xOz.
- Два коэффициента при текущих координатах и свободный член равны нулю. Пусть, например, A=B=D =0. Тогда уравнение плоскости имеет вид Cz =0 или z =0. Эта плоскость проходит через начало координат и параллельна осям Ox и Oy, т. е. уравнение определяет координатнуюплоскость xOy. Аналогично, x =0 – уравнение координатной плоскости yOz и y =0 – плоскость xOz.
|
Date: 2016-08-30; view: 652; Нарушение авторских прав | Понравилась страница? Лайкни для друзей: |
|
|






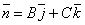 и перпендикулярен оси Ox. Следовательно, плоскость параллельна оси Ox.
и перпендикулярен оси Ox. Следовательно, плоскость параллельна оси Ox.