
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Показатели центральной тенденции
|
|
Ряды распределения численностей, изображенные на рис. 2.5 и 2.7, показывают, что варианты концентрируются около некоторого центрального их значения. Следовательно, можно найти такое значение варианты или абстрактное среднее число, которое будет наиболее представительной характеристикой данной совокупности.
Ряд показателей центральной тенденции включает:
· среднюю арифметическую;
· среднюю квадратическую;
· среднюю геометрическую;
· среднюю гармоническую;
· моду;
· медиану.
Назначение средних величин состоит в том, чтобы отразить какое-нибудь одно свойство совокупности, например, среднюю длину, среднюю массу, средний объем. То свойство (или тот признак) совокупности, которое остается неизменным при замене индивидуальных значений их средним значением, называется определяющим свойством. Средняя отражает определяющее свойство так, что образуемая с ее помощью абстрактная совокупность равных ей чисел по величине определяющего свойства не отличался от реальной.
Средняя арифметическая. Средняя арифметическая - наиболее часто употребляемый статистический показатель центральной тенденции. Она является центром тяжести распределения.
Среднюю арифметическую генеральной совокупности обычно обозначают m, а ее выборочную оценку, т. е. среднюю арифметическую выборочных наблюдений - М (или 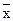 ). Она имеет ту же размерность, что и варианты.
). Она имеет ту же размерность, что и варианты.
Средняя арифметическая получается путем деления суммы всех вариант (x1, x2,..., xn) на объём выборки:
M = (x1+ x2 +... + xn)/N= (Sx)/N, (2.1)
где
N - общее число вариант;
S - знак суммирования.
Без указания в знаке пределов суммирования производится суммирование всех измеренных (наблюденных) вариант ряда от 1 до N.
Пример 2.4. Для вариант (предположим, это высота деревьев, м) 15, 20, 20, 20, 25
M =(15+20+20+20+25)/5 = 100/5 = 20м.
Для ряда, разделенного на классы, т. е. для вариационного ряда, среднюю арифметическую вычисляют как взвешенную величину:
M= (n1x1+ n2x2 +... + nnxn)/N= (Snx)/N, (2.2)
где
x1, x2,..., xn - классовые варианты (срединные значения классов);
n1, n2,..., nn - частоты соответствующих классов;
N - общее число вариант (объем ряда) или общее число наблюдений.
Группируя варианты рассмотренного примера 2.4 по их величине, получим следующий ряд:
| x | |||
| n |
M= (1*15+3*20+ 1*25)/5 = 20 см.
В дальнейшем рассмотрим другие формулы вычисления арифметической средней, основанные на использовании ее основного свойства. Это свойство состоит в том, что сумма отклонений всех вариант от арифметической средней равна нулю. Оно вытекает из содержания средней арифметической как центра тяжести ряда. Сумма вариант, которые больше средней M, равна сумме вариант, которые меньше ее.
Пример 2.5 использована функция СРЗНАЧ() MS Excel для расчета средней арифметической своих аргументов.
Синтаксис: СРЗНАЧ (число1; число2;...), число1, число2,... - это от 1 до 30 аргументов, для которых вычисляется среднее.
Замечания:
· Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.
· Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако, ячейки, которые содержат нулевые значения, учитываются.
· Вычисляя средние значения ячеек, следует учитывать различие между пустыми ячейками и ячейками, содержащими нулевые значения, особенно если не установлен флажок "Нулевые Значения" на панели "Вид" в диалоговом окне "Параметры". Пустые ячейки не учитываются, но нулевые ячейки учитываются. Чтобы открыть диалоговое окно "Параметры", выберите команду "Параметры" в меню "Сервис".
 |
На рис. 2.8 приведено окно программы MS Excel, демонстрирующее применение функции СРЗНАЧ() для определения выборочной средней арифметической M распределения диаметров деревьев сосны, записанных в ячейках А2-А21 (см. пример 2.1). СРЗНАЧ (A2:A21) равняется 35,5 см.
Рис. 2.8.
Средняя геометрическая. При рассмотрении среднего темпа роста изучаемого признака средняя арифметическая не пригодна. Вместо нее вычисляют среднюю геометрическую Mg (или 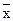 g) по формуле:
g) по формуле:
Mg =  (2.3)
(2.3)
где
x1, x2,..., xn - темпы роста (величины, показывающие, во сколько раз увеличивался признак от периода к периоду);
n -число периодов.
При n >2 формулу удобнее применять в логарифмическом виде:
lgMg = (lgx1+ lgx2 +... + lgxn)/n. (2.4)
Если данные, для которых вычисляют среднюю геометрическую, должны быть взвешены, то формула имеет вид:
lgMg = (n1lgx1+n2 lgx2 +... +nn lgxn)/N. (2.5)
Исходя из содержания формул (2.4) и (2.5), среднюю геометрическую называют также средней логарифмической, так как ее логарифм есть арифметическая средняя логарифмов составляющих величин.
Поясним применение средней геометрической примером.
Пример 2.6. Измеренное растение в конце 1-й, 2-й, 3-й и 4-й декад роста имело объем в дм3: 1, 2, 8, 64.
Относительный темп прироста как отношение результатов двух последовательных наблюдений выразится числами 2/l=2; 8/2=4; 64/8=8. В формулах (2.3)-(2.5) они обозначены x1, x2,..., xn. Средняя геометрическая чисел 2, 4, 8 (n =3) no формуле (2.3) равна:
Mg = 
По формуле (2.4) имеем:
lg Мg = (1/3) (0,3010 + 0,6021 + 0,9031) = 0,6020.
Если бы значения темпа прироста, т. е. варианты 2, 4, 8, были получены на основе разного числа наблюдении, например, соответственно n 1=5, n 2=3, n 3=2, Sn=N =10, то, применяя формулу (2.5), имеем:
lgMg = (5×0,3010 + 3×0,6021 + 2×0,9031)/10 = 0,5118,
Mg = 3,25.
Отметим, что арифметическая средняя из дат 2, 4, 8 равна 4,7
M= 14/3 = 4,7.
Для примера с разными весами этих дат она равна M =3,8, тогда как Mg =3,25.
Проверим пригодность двух видов найденных средних - геометрической и арифметической - для выражения среднего темпа роста. Определяющим свойством здесь будет объем, достигаемый к концу последнего периода. Он равен первоначальному объему, умноженному последовательно на x1, x2, x3, т. е. на числа 2, 4, 8. Эти числа показывают, во сколько раз увеличивался объем за каждый последующий период.
Для примера, в котором каждое значение x получено на основе одного или равного числа наблюдений, истинный объем в конце третьего периода равен 1дм´2´4´8=64 дм3.
Используя среднюю геометрическую, имеем такое же значение объема 1дм´4´4´4=64 дм3.
Применение средней арифметической дает объем к концу третьего периода, равный 1дм´4,7´4,7´4,7 = 103,8 дм3, что не соответствует действительности.
Следовательно, для средней арифметической величины характерно постоянство суммы вариант, а для геометрической средней характерно равенство произведений из первоначальных данных измерений (x1, x2,..., xn) и из геометрических средних Mg1, Mg2,..., Mgn, представленных n раз.
Пример 2.7 использования функции СРГЕОМ () MS Excel для расчета среднего геометрическое значений массива или интервала положительных чисел. Например, функцию СРГЕОМ можно использовать для вычисления средних темпов роста, если задан составной доход с переменными ставками.
Синтаксис: СРГЕОМ (число1;число2;...), где число1, число2,... - это от 1 до 30 аргументов, для которых вычисляется среднее геометрическое. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.
Замечания:
· Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.
· Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки с нулевыми значениями учитываются.
На рис. 2.8 приведено окно программы MS Excel, демонстрирующее применение функции СРГЕОМ() для определения выборочной средней геометрической Mg распределения диаметра деревьев сосны, записанных в ячейках А2-А21 (см. пример 2.1). СРГЕОМ(A2:A21) равняется 35,0.
Средняя квадратическая. В лесном хозяйстве нередко приходится находить сумму площадей сечений деревьев в древостое располагая распределением числа деревьев по ступеням толщины.
Так, для ряда распределения 94 деревьев по ступеням толщины:
| X | |||||||
| N | |||||||
| Sn |
получена сумма площадей сечений всех деревьев равная 69586 см2. Средний арифметический диаметр по формуле (2.2) равен 30,08 см. Площадь сечения g дерева, соответствующая этому диаметру, равна 710,7 см2, а площадь сечений 94 деревьев, найденная как произведение gN=G, составляет 66806 см2. Она на 4% меньше истинной площади сечений.
Такое же расхождение наблюдалось бы и в объеме деревьев. Определяющее свойство - площадь сечения всех деревьев древостоя выражается формулой:
G = (p/4) (n1d12 + n2d22 +…+ nndn2),
где
p =3,14;
n1 n2,..., nn - количество деревьев в ступенях толщины;
d1, d2,..., dn - диаметры ступени толщины, см.
Очевидно, что величина G пропорциональна не диаметрам, а их квадратам.
Поэтому истинная площадь сечений может быть получена через число деревьев и величину среднего квадратического диаметра.
Mq = 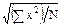 (2.6)
(2.6)
или
Mq =  , (2.7)
, (2.7)
где
x2 - квадраты диаметров;
n - численности деревьев в классах или группах;
N - общее число деревьев в выборке.
Найденный по формуле (2.7) среднеквадратический диаметр равен Mg =30,7 см. Площадь сечения, соответствующая этому диаметру, равна 740,3 см2, а сумма площадей сечений 94 таких деревьев, равна 69586 см2.
Таким образом, для получения истинного значения площади сечений или объемов всех деревьев посредством среднего дерева и числа деревьев диаметр дерева - модели следует находить как среднюю квадратическую величину. В лесной таксации его находят через среднюю арифметическую площадь сечения, что то же самое.
Средняя гармоническая. Для вычисления средней характеристики признаков, которые представляют собой отношение двух других варьирующих величин, пользуются средней гармонической. Среднюю гармоническую определяют по формуле:
Mh = N/(S1/x), (2.8)
или
Mh = N/(Sn/x), (2.9)
где
n - веса отдельных значений.
Так, например, при проведении рубок главного пользования пять лесозаготовительных бригад в одинаковых условиях заготовили за рабочую смену следующие количество древесины (кбм):
1-150, 2-180, 3-130, 4-200, 5-160.
Средняя производительность труда в смену составляет:
Mh = 5/(1/150+1/180+1/130+1/200+1/160) = 160,4.
Мода и медиана. Модой (Мо) называют наиболее часто встречающуюся варианту. В нормально распределенных совокупностях мода численно равна средней арифметической.
В положительно асимметричных рядах Мо > М, а в отрицательно асимметричных Мо < М.
В ряду:
| X | |||||||
| n |
Mo =28 см.
Медианой (Mе) называют значение признака, занимающее срединное положение в ряду и делящее все распределение на две равные по численности части.
Среди значений 5; 6; 7; 8; 9 Mе = 7.
Для вариационного ряда
Me = x0 + k [ (S1-S2) / n ], (2.10)
где
x0 - значение нижней границы класса, в котором содержится половина накопленных частот;
k - интервал;
S1 - полусумма общей численности ряда, S1 =N/2;
S2 - накопленная частота, предшествующая группе, в которой находится медиана.
Для ряда распределения 94 деревьев по ступеням толщины Ме = 30
| X | |||||||
| n | |||||||
| Sn |
Me = 26 + 4 [(47 - 19)/28] = 30 см.
Пример 2.8 использования функции МОДА() и МЕДИАНА() MS Excel для расчета моды и медианы, которые являются характеристиками центральной тенденции выборки. Они не имеют своего аналога в генеральной совокупности и поэтому рассматриваются как показатели относительного характера.
Функция МОДА() возвращает наиболее часто встречающееся или повторяющееся значение в массиве или интервале данных. Так же, как и функция МЕДИАНА, функция МОДА является мерой взаимного расположения значений.
Синтаксис: МОДА (число1;число2;...), где число1, число2,... - это от 1 до 30 аргументов, для которых вычисляется мода. Можно использовать один массив или одну ссылку на массив вместо аргументов, разделяемых точкой с запятой.
Замечания:
· Аргументы должны быть числами, именами, массивами или ссылками, которые содержат числа.
· Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.
В наборе значений мода - это наиболее часто встречающееся значение; медиана - это значение в середине массива; среднее - это среднее арифметическое значение. Ни одно из этих чисел не характеризует в полной мере то, в какой степени центрированы данные. Пусть данные сгруппированы в трех областях, одна половина данных близка к некоторому малому значению, а другая половина данных близка к двум другим большим значениям. Обе функции СРЗНАЧ и МЕДИАНА могут вернуть значение из относительно пустой середины, а функция МОДА скорее всего вернет доминирующее малое значение. МОДА ({5,6; 4; 4; 3; 2; 4}) равняется 4.
Функция МЕДИАНА() возвращает медиану заданных чисел. Медиана - это число, которое является серединой множества чисел, то есть половина чисел имеет значения большие, чем медиана, а половина чисел имеет значения меньшие, чем медиана.
Синтаксис: МЕДИАНА (число1;число2;...), где число1, число2,... - это от 1 до 30 чисел, для которых определяется медиана.
Замечания:
· Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа. Microsoft Excel проверяет все числа, содержащиеся в аргументах, которые являются массивами или ссылками.
· Если аргумент, который является ссылкой, содержит пустые ячейки, текстовые или логические значения, то такие значения игнорируются; однако, ячейки, которые содержат нулевые значения, учитываются.
· Если в множестве четное количеств чисел, то функция МЕДИАНА вычисляет среднее двух чисел, находящихся в середине множества. См. второй из следующих примеров.
Примеры:
МЕДИАНА (1; 2; 3; 4; 5) равняется 3.
МЕДИАНА (1; 2; 3; 4; 5; 6) равняется 3,5, среднее 3 и 4.
Расчет Mo и Me с использованием MS Excel для исходных данных примера 2.1 представлены на рис. 2.8.
Показатели вариации
Средняя величина не дает достаточного представления о свойствах изучаемой совокупности. Являясь показателем центральной тенденции, т. е. наиболее представительной характеристикой изучаемого объекта, она не характеризует степени разнообразия (изменчивости, варьирования) составляющих его единиц. Действительно, ряды из вариант 1, 3, 4, 5, 7 и 3, 4, 4, 4, 5 характеризуются одинаковой средней арифметической х =4, но отличаются по степени вариации значений признака.
Определение меры изменчивости признака или качества рассматриваемого объекта или явления считается не менее важной задачей, чем характеристика средних величин. Более того, доверие к средней величине может быть определено лишь постольку, поскольку дана оценка варьированию величин в рассматриваемой совокупности вариант.
Главной целью статистических методов является выявление вариации, которая характеризуется рядом показателей:
· размах варьирования;
· дисперсия;
· среднее квадратическое отклонение;
· коэффициент вариации.
Размах варьирования. Разность между наибольшим и наименьшим значением признака называется размахом, который является грубым показателем варьирования признака. В двух вышеприведенных рядах, состоящих из пяти вариант, он равен 7-1=6 и 5-3=2, т. е. указывает, что в общем вариация в первой группе цифр в 3 раза больше, чем во второй. Однако, опираясь лишь на два крайних члена ряда, величина размаха не учитывает внутреннего, между этими крайними значениями, рассеяния вариант. Кроме того, крайние значения как редко встречающиеся члены ряда весьма неустойчивы по своему размеру и сильно зависят от объема выборочных наблюдений. Несмотря на это, при малых выборках, повторяемых несколько раз, размах варьирования нашел широкое применение.
Среднее квадратическое отклонение и дисперсия. Основным показателем вариации (изменчивости) считается среднее квадратическое отклонение, которое определяется как корень квадратный из средней арифметической квадратов отклонений вариант от их средней арифметической величины.
Среднее квадратическое отклонение для выборки обозначают через s, а для генеральной совокупности -s. Согласно определению:
s =  =
= 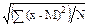 , (2.11)
, (2.11)
В математической статистике оперируют средним квадратом отклонений (s2 для выборки и s2 для генеральной совокупности), называемым дисперсией, которая рассчитывается по формуле (2.12).
s2 =  =
= 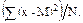 (2.12)
(2.12)
Для расчетов по вариационному ряду среднее квадратическое отклонение выразится формулой:
s =  =
=
= 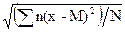 , (2.13)
, (2.13)
а дисперсия
s2 =  =
=
= 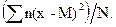 (2.14)
(2.14)
В уравнениях (2.11-2.14)
x1, x2,..., xn - варианты ряда (средние значения классов);
M - средняя арифметическая;
n1, n2,..., nn - частоты в классах;
N - общий объем ряда.
Оценивая величину s по выборочному значению s, при обработке выборки с числом наблюдений N меньше 100 в качестве делителя в формулах (2.11) - (2.14) принимают не N, а N -1. Это число называют числом степеней свободы. Такое название объясняется тем, что в статистике при вычислении любых средних величин используют число независимых величин. При вычислении s одно из отклонений оказывается несвободным. Оно равно сумме всех остальных, взятых с обратным знаком.
Таким образом, общей формулой для нахождения среднего квадратического отклонения будет:
s = 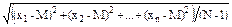 =
= 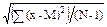 , (2.15)
, (2.15)
а для дисперсии
s2 = 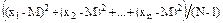 =
=  (2.16)
(2.16)
При обработке вариационных рядов формулы принимают вид:
s = 
 =
=
=  , (2.17)
, (2.17)
 s2 =
s2 = 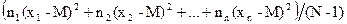 =
=
=  (2.18)
(2.18)
Среднее квадратическое отклонение называется также стандартным отклонением. Полученная величина является именованной и выражается в тех же единицах измерения, что и отдельные значения признака.
Средняя величина M и среднее квадратическое отклонение s дают полную количественную характеристику любой эмпирической совокупности, подчиняющейся закону нормального распределения. Средняя арифметическая отображает действие на признак основных факторов. Среднее квадратическое отклонение, характеризующее варьирование значений признака вокруг центра распределения, является мерой степени влияния на признак различных второстепенных причин, вызывающих варьирование.
В результате действия этих причин наиболее частыми будут варианты с небольшими отклонениями. Чем отклонения больше, тем варианты встречаются реже. Это положение подробно рассмотрено в учебной литературе при анализе свойств нормального распределения вероятностей случайного события x. В статистических совокупностях с нормальным (или близким к нормальному) распределением частот 68,3% вариант имеют значения, не превосходящие m ±s и только 31,7% вариант по своей величине выходят за эти пределы. Отсюда вероятность того, что любая взятая наугад варианта ряда находится вне пределов m± s равна 0,317. За пределами m±2 s лежит всего 4,5%, а за пределами m±3 s - 0,3% общего числа вариант. Следовательно, вероятность того, что взятая наугад варианта ряда окажется отклоняющейся от m на величину, большую 2 s и З s, соответственно равна 0,045 и 0,003.
Пример 2.9 использования функции ДИСП () MS Excel для оценивания дисперсии по выборке.
Синтаксис: ДИСП (число1;число2;...), где число1, число2,... - это от 1 до 30 числовых аргументов, соответствующих выборке из генеральной совокупности.
Замечания:
· ДИСП предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, вычисляйте дисперсию, используя функцию ДИСПР.
· Логические значения, такие, как ИСТИНА или ЛОЖЬ, а также текст игнорируются. Если они не должны игнорироваться, пользуйтесь функцией рабочего листа ДИСПА.
Пример. На рис. 2.7 приведено окно программы MS Excel, демонстрирующее применение функции ДИСП() для определения выборочной средней арифметической s2 распределения диаметров деревьев, записанных в ячейках А2-А21 (см. пример 2.1).
ДИСП (A2:A21) равняется 34,5 см2.
Коэффициент вариации. Коэффициент вариации, как и s или s, является показателем изменчивости признака, выражая ее в относительных единицах. Он представляет собой среднее квадратическое отклонение отдельных вариант ряда от средней величины, выраженное в процентах:
v = (s / M) 100%. (2.19)
Являясь показателем, не зависящим от принятых единиц измерения вариант, коэффициент вариации может применяться для сравнительной оценки величины варьирования различных признаков. Вместе с тем он в значительной степени зависит от величины средней арифметической, и поэтому его применение должно быть ограничено случаями, когда имеет место естественное от нуля начало отсчета или когда ряды распределения имеют сходные начала отсчета.
Коэффициент дифференциации. Устранить указанное ограничение позволяет коэффициент дифференциации, который без группировки вариант в классы рассчитывается по формуле:
 . (2.20)
. (2.20)
Для совокупностей со сгруппированными вариантами формула принимает вид:
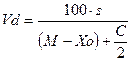 , (2.21)
, (2.21)
где
Xo – значение первого класса ряда распределения;
С – ширина классового промежутка.
При начале ряда распределения в пересечении осей координат, величины коэффициентов вариации и дифференциации совпадают.
Поскольку в лесоводственных и таксационных исследованияхдля нормальной кривой распределения применяется вероятность 0,99865 (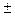 3 s), то на ее основе разработана классификация степени дифференциации:
3 s), то на ее основе разработана классификация степени дифференциации:
Величина коэффициента Степень дифференциации
дифференцаации
до 13% слабая
14 - 27% умеренная
28 –38%средняя (нормальная)
39- 53% значительная
54-70% большая
более 70% очень большая
Date: 2016-07-25; view: 692; Нарушение авторских прав