Определение предела функции в точке по Коши

Число называется пределом функции в точке , если она определена в некоторой проколотой окрестности точки и если для любого сколь угодно малого числа можно указать такое число что для всех х:

, выполнено неравенство .

.

Если – предел функции в точке , то это записывают так:

или .

Односторонние пределы функции в точке. Назовем левой полуокрестностью точки произвольный интервал а правой полуокрестностью точки – произвольный интервал .

Число А называется пределом функции в точке справа (слева), если функция определена в некоторой правой (левой) полу-окрестности точки и если для любой последовательности , , 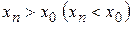сходящейся к ,соответствующая последовательность значений функции сходится к А. Односторонние пределы обозначают:

– предел справа,

– предел слева.

Заметим, что односторонние пределы могут не совпадать.

Пример 1. Найти предел функции:

а) ;

б)

Пример 2. Найти односторонние пределы функции в точке :

Date: 2016-07-25; view: 337; Нарушение авторских прав