Предел последовательности

Минченков, Ю. В.

М 62 Высшая математика. Сборник задач по математическому анализу: учеб.-метод. пособие / Ю. В. Минченков.– Минск: Частн. ин-т упр. и предпр., 2008.– 83 с.

ISBN 978-985-6877-23-3.

Приведены формулы, определения и другие краткие пояснения теории, необходимые для решения задач. Сборник содержит типовые задачи по математическому анализу с решениями и пояснениями.

Предназначен для самостоятельной работы студентов Частного института управления и предпринимательства.

УДК 51

ББК 22.1я73

© Минченков Ю. В., 2008

ISBN 978-985-6877-23-3 © Частный институт управления и предпринимательства, 2008

ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ

Бесконечной числовой последовательностью (или просто последовательностью) называется функция

(1)

определенная на множестве натуральных чисел. Каждое значение называют элементом (или членом) последовательности, а число п – номером элемента последовательности. Заметим, что последовательность всегда содержит бесконечное число членов.

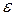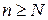Число а называется пределом числовой последовательности при , если для любого положительного сколько угодно малого числа существует номер , такой, что для всех выполняется неравенство

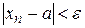. (2)

Обозначается .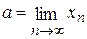

Математически данное определение можно записать в виде:

.

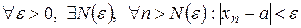Числовая последовательность, имеющая конечный предел, называется сходящейся. Последовательность, не имеющая предела, называетс я рас-ходящейся. Если 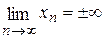, то говорят, что последовательность сходится к бесконечности.

Пример 1. Доказать, что число 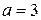является пределом последовательности . Найти, сколько элементов данной последовательности не попало в 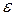-окрестность числа 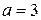, если .

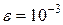Решение. Из неравенства (2) следует

Таким образом, (целая часть числа, так как 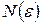– это номер элемента). Следовательно, при
, т. е. число 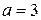является пределом данной числовой последовательности.

Пусть Следовательно, ровно 1999 элементов находится за пределами интервала .

,

.

Числовая последовательность называется бесконечно большой последовательностью (б.б.п.), если .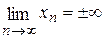

Числовая последовательность называется бесконечно малой последовательностью (б.м.п.), если .

Date: 2016-07-25; view: 314; Нарушение авторских прав