Показательная функция. Степень с иррациональным показателем.

Зафиксируем положительное число а и поставим в соответствие каждому числу 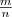число 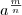. Тем самым получим числовую функцию f(x) = a^x, определенную на множестве Q рациональных чисел и обладающую ранее перечисленными свойствами. При а=1 функция f(x) = a^xпостоянна, так как 1^x=1 для любого рационального х.

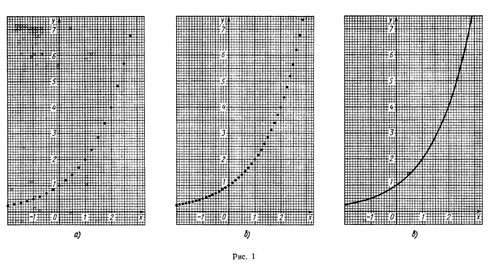
Нанесем несколько точек графика функции у =2^x предварительно вычислив с помощью калькулятора значения 2^x на отрезке [—2; 3] с шагом 1/4 (рис. 1, а), а затем с шагом 1/8 (рис. 1, б).Продолжая мысленно такие же построения с шагом 1/16, 1/32 и т. д., мы видим, что получающиеся точки можно соединить плавной кривой, которую естественно считать графиком некоторой функции, определенной и возрастающей уже на всей числовой прямой и принимающей значения 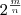в рациональных точках 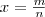(рис. 1, в). Построив достаточно большое число точек графика функции 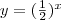, можно убедиться в том, что аналогичными свойствами обладает и эта функция (отличие состоит в том, что функция 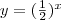убывает на R).

Эти наблюдения подсказывают, что можно так определить числа 2^α и 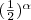для каждого иррационального α, что функции, задаваемые формулами y=2^x и 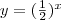будут непрерывными, причем функция у=2^x возрастает, а функция 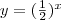убывает на всей числовой прямой.

Опишем в общих чертах, как определяется число a^α для иррациональных α при а>1. Мы хотим добиться того, чтобы функция у = a^x была возрастающей. Тогда при любых рациональных r₁ и r₂, таких, что r₁<α<r₂, значение a^α должно удовлетворять неравенствам a^r₁<а^α<а^r₁.

Выбирая значения r₁ и r₂, приближающиеся к х, можно заметить, что и соответствующие значения a^r₁ и a^r₂ будут мало отличаться. Можно доказать, что существует, и притом только одно, число у, которое больше всех a^r₁ для всех рациональных r₁и меньше всех a^r₂ для всех рациональных r₂. Это число у по определению есть а^α.

Например, вычислив с помощью калькулятора значения 2^x в точках х_n и х`<sub>n</sub>, где х<sub>n</sub> и х`_n — десятичные приближения числа 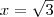мы обнаружим, что, чем ближе х_n и х`<su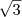b>n</sub> к , тем меньше отличаются 2<sup>x</sup><sub>n</sub> и 2<sup>x`</sup>_n.

Так как 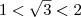, то

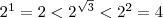
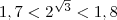и, значит,

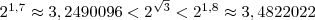
Аналогично, рассматривая следующие десятичные приближения 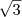по недостатку и избытку, приходим к соотношениям

;

;

;

;

.

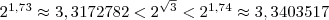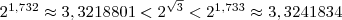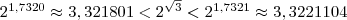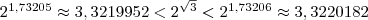Значение 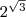вычисленное на калькуляторе, таково:

.

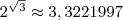Аналогично определяется число a^α для 0<α<1. Кроме того полагают 1^α=1 для любого α и 0^α=0 для α>0.

Date: 2016-07-25; view: 710; Нарушение авторских прав