Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Распределение Пуассона
|
|
Вернемся к распределению Пуассона. Возможными значениями случайной величины X с распределением Пуассона являются числа 0,1,2,...; а их вероятности определяются так 
, m=1,2,...; Распределение Пуассона определяется одним параметром а.
Отметим следующее: математическое ожидание и дисперсия случайной величины с распределением Пуассона равны между собой и раны параметру распределения а.
Несложно устанавливается, что распределение Пуассона является пределом биноминального распределения при 
.Отсюда при малом p и n достаточно большом, а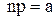 
имеем приближенную формулу
.
То есть, распределение Пуассона выражает закон распределения числа появлений маловероятных событий при большом числе испытаний. Поэтому иногда распределение Пуассона называют законом малых чисел. Значения обычно определяют по таблице, имеются специальные таблицы для определения этих значений для конкретных m и a.
Закон распределения Пуассона существенно используется при исследовании обрывности нити. В.П. Левинским и А.Б. Мякиной было установлено, что технологическая обрывность, т.е., число обрывов на 1000 веретен в час при налаженном технологическом процессе, приближенно подчиняется распределению Пуассона. Поэтому, прежде всего, соотношение M(X)=D(X)=a является критерием технологической обрывности, не выполнение этого условия может быть свидетельством того, что обрывность обусловлена нетехнологической обрывностью, т.е. неполадками производственного характера (неисправностью веретен, некачественным обслуживанием и т.д.).
Пример 1. Мотальщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение 1 мин равна 0,003. Определить вероятность того, что в течение 1 мин обрывы произойдут:
1) на 4 веретенах; 2) не более чем на 4 веретенах.
Итак, n=1000; р=0,003; 
.По формуле , применяя специальную таблицу находим 
Далее используя теорему сложения вероятностей определим
Теперь рассмотрим задачу такого типа. Прядильщица за длительный промежуток времени T в среднем ликвидирует в минуту 
обрывов. Следует определить вероятность того, что в течение времени t мин ликвидирует m обрывов. Как известно, эта задача сводится к применению асимптотической формулы Пуассона:
.
Пример 2. Прядильщица в среднем ликвидирует 180 обрывов в течение часа на 1000 веретен. Определить вероятность того, что в течение 2 мин потребуется ликвидировать 4 обрыва.
Имеем 
.
Итак, по вышеприведенной формуле будем иметь
.
Заключение. Пусть случайная величина Х имеет биноминальное распределение.
1. Если число испытаний n небольшое, то вероятности возможных значений целесообразно найти по формуле Бернулли
.
2. Если число испытаний n достаточно большое, то вероятности возможных значений определяются по локальной формуле Муавра - Лапласа
.
3. При малом p и n достаточно большом используют асимптотическую формулу Пуассона
, где a = np.
8. Контрольная работа №2 по теории вероятностей
Задача 1. Дискретная случайная величина дана таблицей распределения вероятностей. Найти: функцию распределения F(x) и построить график этой функции M(X), D(X), 
, V(X), 
;
Вариант 1
| x | |||
| P | 0,7 | 0,2 |
Вариант 2
| X | ||||
| P | 0,5 | 0,2 | 0,1 |
Вариант 3
| x | |||
| P | 0,4 | 0,1 |
Вариант 4
| X | ||||
| P | 0,3 | 0,1 | 0,2 |
Вариант 5
| x | |||
| P | 0,3 | 0,1 |
Вариант 6
| X | ||||
| P | 0,4 | 0,2 | 0,2 |
Вариант 7
| x | |||
| P | 0,3 | 0,1 |
Вариант 8
| X | ||||
| P | 0,3 | 0,2 | 0,1 |
Вариант 9
| x | |||
| P | 0,6 | 0,1 |
Вариант 10
| X | ||||
| P | 0,3 | 0,2 | 0,1 |
Задание 2.
Вариант 1. Непрерывная случайная величина X дана дифференциальной функцией распределения
1. Найти интегральную функцию распределения F(x), M(X), D(X), , V(X), 
; 2. Построить графики функций f(x) и F(x).
Вариант 2. Непрерывная случайная величина X дана дифференциальной функцией распределения
1. Найти интегральную функцию распределения F(x), M(X), D(X), , V(X), 
; 2. Построить графики функций f(x) и F(x).
Вариант 3. Непрерывная случайная величина X дана дифференциальной функцией распределения
1. Найти интегральную функцию распределения F(x), M(X), D(X), , V(X), 
; 2. Построить графики функций f(x) и F(x).
Вариант 4. Непрерывная случайная величина X дана дифференциальной функцией распределения
1. Найти интегральную функцию распределения F(x), M(X), D(X), , V(X), 
; 2. Построить графики функций f(x) и F(x).
Вариант 5. Непрерывная случайная величина X дана дифференциальной функцией распределения
1. Найти интегральную функцию распределения F(x), M(X), D(X), , V(X),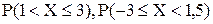 
; 2. Построить графики функций f(x) и F(x).
Вариант 6. Непрерывная случайная величина X дана дифференциальной функцией распределения
1. Найти интегральную функцию распределения F(x), M(X), D(X), , V(X),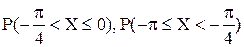 
; 2. Построить графики функций f(x) и F(x).
Вариант 7. Непрерывная случайная величина X дана дифференциальной функцией распределения
1. Найти интегральную функцию распределения F(x), M(X), D(X), , V(X), 
; 2. Построить графики функций f(x) и F(x).
Вариант 8. Непрерывная случайная величина X дана дифференциальной функцией распределения
1. Найти интегральную функцию распределения F(x), M(X), D(X), , V(X), 
; 2. Построить графики функций f(x) и F(x).
Вариант 9. Непрерывная случайная величина X дана дифференциальной функцией распределения
1. Найти интегральную функцию распределения F(x), M(X), D(X), , V(X), 
; 2. Построить графики функций f(x) и F(x).
Вариант 10. Непрерывная случайная величина X дана дифференциальной функцией распределения
1. Найти интегральную функцию распределения F(x), M(X), D(X), , V(X), 
; 2. Построить графики функций f(x) и F(x).
Задание 3.
1. Прочность образцов пряжи, как случайная величина, приближенно подчиняется нормальному закону распределения. Средняя прочность равна 240 сн, 
. Определить долю образцов пряжи, обладающих прочностью от 200 сн до 250 сн.
2. Прочность 50 – миллиметровых образцов ровницы, как случайная величина, приближенно подчиняется нормальному закону распределения. Средняя прочность равна 230 сн, 
. Определить долю образцов пряжи, обладающих прочностью от 180 сн до 250 сн.
3. Швейная фабрика выпускает мужские костюмы для некоторого региона, где средний рост взрослых мужчин равен 171,2 см, 
. Определить процент удовлетворенности населения, если ограничиться выпуском костюмов, соответствующих ростам от 166 см до 189 см.
4. В результате антропологических исследований населения некоторого региона было установлено, что средний обхват груди мужчин равен 95,1 см, 
. Определить долю мужчин в этом регионе, имеющих обхват груди от 86 см до 105 см.
5. Средний рост девочек от 14-16 лет некоторого региона равен 160, 2 см, 
Какой процент всех девочек имеет рост, отклоняющийся от среднего значения в ту или другую сторону на н 5 см.
6. Средний обхват груди взрослого женского населения некоторого региона равен 102,3см, 
(коэффициент вариации). Какой процент всех женщин имеет обхват груди, отклоняющийся от среднего значения в ту или другую сторону на 4 см.
7. Прочность образцов пряжи, как случайная величина, приближенно подчиняется нормальному закону распределения. Средняя прочность равна 230 сн, 
. Определить долю образцов пряжи, обладающих прочностью от 210 сн до 260 сн.
8. Прочность 50 – миллиметровых образцов ровницы, как случайная величина, приближенно подчиняется нормальному закону распределения. Средняя прочность равна 220 сн, 
. Определить долю образцов пряжи, обладающих прочностью от 185 сн до 245
9. Швейная фабрика выпускает мужские костюмы для некоторого региона, где средний рост взрослых мужчин равен 173,1 см, 
. Определить процент удовлетворенности населения, если ограничиться выпуском костюмов, соответствующих ростам от 165 см до 190 см.
10. В результате антропологических исследований населения некоторого региона было установлено, что средний обхват груди мужчин равен 92,3 см, 
. Определить долю мужчин в этом регионе, имеющих обхват груди от 84 см до 106 см.
Задание 4.
Вариант 1. Смесь состоит из хлопка и шерсти в пропорции 3:2. Пусть X- число хлопковых волокон в случайном соединении 5 волокон.
1) Составить закон распределения случайной величины X. 2) Найти M(X); D(X); ; P(2<X<5).
Вариант 2. Смесь состоит из 20% хлопка и 80% шерсти.. Пусть X- число хлопковых волокон в случайном соединении 5 волокон.
1) Составить закон распределения случайной величины X. 2) Найти M(X); D(X); ; 
.
Вариант 3. Смесь состоит из хлопка и лавсана в пропорции 1:3. Пусть X- число шерстяных волокон в случайном соединении 6 волокон.
1) Составить закон распределения случайной величины X. 2) Найти M(X); D(X); ; 
.
Вариант 4. В ящике большое количество катушек с нитками разных цветов, из них 40% черных. Пусть X- число катушек с нитками черного цвета среди 7 наугад взятых катушек.
1) Составить закон распределения случайной величины X. 2) Найти M(X); D(X); ; 
.
Вариант 5. В ящике большое количество початков с крашеной и некрашеной пряжей в пропорции 1:4. Пусть X- число початков с крашеной пряжей среди 6 наугад взятых початков.
1) Составить закон распределения случайной величины X. 2) Найти M(X); D(X); ; 
.
Вариант 6. На швейную фабрику поступает товар с двух ткацких фабрик в пропорции 1:3. Пусть X- число кусков товара, сработанных первой фабрикой, среди 5 наугад взятых кусков.
1) Составить закон распределения случайной величины X. 2) Найти M(X); D(X); ; .
Вариант 7. Швейная фабрика выпускает 40% пальто 50 размера. Пусть X- число пальто 50 размера среди 6 случайно отобранных пальто.
1) Составить закон распределения случайной величины X. 2) Найти M(X); D(X); ; 
.
Вариант 8. Смесь состоит из хлопка и шерсти в пропорции 3:5. Пусть X- число хлопковых волокон в случайном соединении 4 волокон.
1) Составить закон распределения случайной величины X. 2) Найти M(X); D(X); ; P(2<X).
Вариант 9. В ящике большое количество катушек с нитками разных цветов, из них 60% черных. Пусть X- число катушек с нитками черного цвета среди 6 наугад взятых катушек.
1) Составить закон распределения случайной величины X. 2) Найти M(X); D(X); ; 
.
Вариант 10. Швейная фабрика выпускает 25% костюмов 52 размера. Пусть X- число костюмов 52 размера среди 5 случайно отобранных костюмов.
1) Составить закон распределения случайной величины X. 2) Найти M(X); D(X); ; .
Задание 5.
Вариант 1. Вероятность того, что деталь не прошла ОТК, равна р=0,4. Определить вероятность того, что среди 200 случайно отобранных деталей:
1) непроверенных окажется ровно 10 деталей; 2) непроверенных от 20 до 50.
Вариант 2. Вероятность появления события А в каждом испытании равна р=0,2. Определить вероятность того, что при 200 испытаниях событие А появится: 1) ровно 30 раз; 2) 40 до 100.
Вариант 3. В цехе швейной фабрики имеется 50 машин. Вероятность замены некоторой детали за время Т равна 0,2. Определить вероятность того, что наличие восьми таких запасных деталей обеспечит бесперебойную работу цеха из-за их отсутствия в течение времени Т.
Вариант 4. В швейном цехе имеется 50 машин. Вероятность замены некоторой детали за время Т равна 0,2. Сколько следует иметь в запасе этих деталей, чтобы с вероятностью 0,954 обеспечить бесперебойную работу всего цеха в течение времени Т?
Вариант 5. Смесь состоит из хлопка и шерсти в пропорции 3:5. Пусть X- число хлопковых волокон в случайном соединении 100 волокон.
1) Определить 
. 2) Найти наивероятнейшее число, а также вероятность этого числа.
Вариант 6. Известно, что 80% ткани выдерживает гарантийный срок на износостойкость. Определить вероятность того, что из 400 образцов ткани число выдержавших этот строк: 1) равен 60; 2) от 60 до 100.
Вариант 7. Швея в среднем изготовляет 70% изделий первого сорта. Пусть Х-число изделий первого сорта среди случайно отобранных 120 изделий.
1) Определить 
. 2) Найти наиболее вероятное число изделий первого сорта, а также вероятность этого числа.
Вариант 8. В швейном цехе имеется 100 машин. Вероятность того, что за время Т сломается одна игла равна 0,08. Сколько следует иметь запасных игл, чтобы с вероятностью 0,954 обеспечить бесперебойную работу всех машин?
Вариант 9. В цехе находятся 160 однотипных станков. Вероятность того, что в течение времени Т остановится каждый станок равна 0,25. Пусть Х- число остановившихся станков за время Т. Определить 
.
2) Найти наивероятнейшее число, а также вероятность этого числа.
Вариант 10. В ткацком цехе 100 станков. Вероятность того, что за время Т какой-нибудь из челноков требует замены, рана 0,12.. Сколько следует иметь запасных челноков, чтобы с вероятностью 0,954 обеспечить бесперебойную работу всех станков в течение времени Т?
Задание 6.
1. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение 1 мин равна 0,004. Определить вероятность того, что в течение 1 мин обрывы произойдут: на 5 веретенах; 2) не более чем на 6 веретенах.
2. Прядильщица в среднем ликвидирует 120 обрывов в течение часа на 1000 веретен. Определить вероятность того, что в течение 3 мин потребуется ликвидировать 1) 4 обрыва; 2) менее 5 обрывов.
3. Прядильщица обслуживает 500 веретен. Вероятность обрыва нити на одном веретене в течение 1 мин равна 0,006. Определить вероятность того, что в течение 1 мин обрывы произойдут:
2) на 4 веретенах; 2) более чем на 3 веретенах.
4. Прядильщица в среднем ликвидирует 120 обрывов в течение часа на 500 веретен. Определить вероятность того, что в течение 4 мин потребуется ликвидировать 1) 3 обрыва; 2) более 3 обрывов.
5. Мотальщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение 1 мин равна 0,003. Определить вероятность того, что в течение 1 мин обрывы произойдут: на 6 веретенах; 2) не более чем на 4 веретенах.
6. Прядильщица в среднем ликвидирует 180 обрывов в течение часа на 1000 веретен. Определить вероятность того, что в течение 2 мин потребуется ликвидировать 1) 3 обрыва; 2) менее 4 обрывов.
7. Прядильщица обслуживает 800 веретен. Вероятность обрыва нити на одном веретене в течение 1 мин равна 0,005. Определить вероятность того, что в течение 1 мин обрывы произойдут: на 6 веретенах; 2) более чем на 4 веретенах.
8. Прядильщица в среднем ликвидирует 120 обрывов в течение часа на 500 веретен. Определить вероятность того, что в течение 3 мин потребуется ликвидировать 1) 2 обрыва; 2) более 4 обрывов.
9. Мотальщица обслуживает 500 веретен. Вероятность обрыва нити на одном веретене в течение 1 мин равна 0,008. Определить вероятность того, что в течение 1 мин обрывы произойдут: на 7 веретенах; 2) не более чем на 8 веретенах.
10. Прядильщица в среднем ликвидирует 90 обрывов в течение часа на 1000 веретен. Определить вероятность того, что в течение 4 мин потребуется ликвидировать 1) 8 обрыва; 2) менее 8 обрывов.
Основная литература
1. Пискунов Н.С. Дифференциальное и интегральное исчисление. - М.: Наука, т.1, 1985.- 429 с.
2. Пискунов Н.С. Дифференциальное и интегральное исчисление. - М.: Наука, т.2, 1985.- 560 с.
3. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. – М.: Наука, 1980. – 432 с.
4. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальные уравнения, кратные интегралы, ряды, функции комплексного переменного. – М.: Наука, 1985. – 464 с.
5. Артюнов Ю.С., Полозков А.П. Высшая математика. Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений. –М.: Высшая школа, 1985. -144 с.
6. Сборник задач по математике. Линейная алгебра и основы математического анализа.- М.: Наука, под редакцией А.В.Ефимова и Б.П. Демидовича, 1986 –464 с.
7. Сборник задач по математике. Для втузов. Специальные разделы математического анализа. -М.: Наука, под редакцией В.Ефимова и Б.П. Демидовича. 1986 – 366 с.
8. В.Е. Гмурман. Руководство к решению задач по теории вероятностей и математической статистике. Москва, высшая школа, 2002.
9. В.Е. Гмурман. Теория вероятностей и математическая статистика. Москва, высшая школа, 1998.
10. Н.Ш. Кремер. Высшая математика для экономистов. Москва, 2000.
11. Под редакцией Ермакова. Сборник задач по высшей математике для экономистов. Москва, ИНФРА, 2001
Дополнительная литература
1. Задачи и упражнения по математическому анализу для втузов / Под редакцией Б.П. Демидовича. - М.: Наука, 1964-1978. – 472 с.
2. Кудрявцев Л.Д. Математический анализ. – М: Высшая школа, 1970 – 592 с.
3. Кудрявцев Л.Д. Математический анализ. – М: Высшая школа, 1981 – 584 с.
4. Бермант А.Ф., Арамонович И.Г. Краткий курс математического анализа. - М.: Наука, 1969. – 736 с.
5. В.П. Чистяков. Курс теории вероятностей. М.: Наука, 1987.
6. Б.В. Гнеденко. Курс теории вероятностей. М.:Наука,1988.
7. Б.А.Севастьянов, В.П.Чистяков, А.М.Зубов. Сборник задач по теории вероятностей. М.:Наука,1980
СОДЕРЖАНИЕ
ВВЕДЕНИЕ…………………………………………………………………..3
Г Л А В А 1. Дифференциальное исчисление функции многих
переменных...................................................................................................... 3
1.1. Краткие теоретические сведения и упражнения…………………………..3
1.2. Упражнения для самостоятельной работы…………………………….... 17
1.3. Задачи для контрольной работы…………………………………………. 21
Г Л А В А 2. Дифференциальные уравнения ……………………..32
2.1 Дифференциальные уравнения первого порядка……………………...32
1. Основные понятия и теоретические сведения…………………….... 32
2. Особые решения……………………………………………………….. 35
3. Интегрирование дифференциальных уравнений первого.
порядка…………………………………………………………………. 37
2.2 Дифференциальные уравнения высших порядков……………………. 56
1. Уравнения, допускающие понижение порядка…………………….. 56
2. Линейные дифференциальные уравнения с постоянными
Коэффициентами……………………………………………………….. 61
2. 3 Системы дифференциальных уравнений…………………………….. 66
2. 4 Задачи на составление дифференциальных уравнений…………….. 70
2. 5 Упражнения для самостоятельной работы………………………….. 72
2. 6 Задания для контрольной работы……………………………….. …. 73
Г Л А В А 3. Теория вероятностей …………………………………..86
3.1. Основные понятия …………………………………………………………86
1. Алгебра событий ………………………………………………………….86
2. Вероятностное пространство ……………………………………………88
3. Теоремы сложения и умножения вероятностей ………………………. 89
4. Независимость событий…………………………………………………. 90
5. Классическое вероятностное пространство …………………………… 90
6. Элементы комбинаторики …. ……………………………………………90
7. Геометрические вероятности …………………………………………… 92
8. Упражнения и задачи ……………………………………………………. 93
9. Формула полной вероятности и Байеса ………………………………... 96
10. Схема Бернулли …. …………………………………………………….. 99
3.2. Контрольная работа № 1 по теории вероятностей……………………. 102
3.3. Случайные величины……………………. ………………………………108
1. Понятие случайной величины…………………………………………..108
2. Дискретные случайные величины……………………………….…..…108
3. Примеры дискретных случайных величин …. ………………………..109
4. Непрерывные случайные величины …………………………………. 110
5. Числовые характеристики случайных величин………..……………...112
6. Формула Лапласа ………………………………………………………. 118
7. Распределение Пуассона ……………………………………………….121
8. Контрольная работа № 1 по теории вероятностей ……………….....123
Date: 2016-07-25; view: 3074; Нарушение авторских прав