Глава III. Теория вероятностей

Основные понятия

Алгебра событий

Произвольное множество будем называть пространством элементарных событий. Элементы 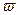этого множества назовем элементарными событиями. Эти понятия являются первоначальными. В реальном опыте элементы 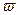интерпретируются как взаимно исключающие исходы изучаемого случайного явления. Для описания каждой реальной задачи множество выбирается наиболее подходящим образом. Приведем ряд примеров поясняющих выбор множества .

1. Пусть монета подбрасывается один раз. При бросании монеты возможны исходы: выпадение герба, выпадение “Решетки“. Итак, при описании этого опыта мы полагаем ={ }, где соответственно означают выпадение герба и выпадение решетки.

2. Теперь рассмотрим подбрасывание игральной кости, т.е., однородного кубика, на каждой грани которого написано различное число от 1 до 6. Естественно в этом случае следует выбрать ={ }, где (к=1,2,…,6) означают исход опыта, заключающийся в выпадении к очков. Имеем шесть исключающих друг друга исходов.

3. Далее рассмотрим подбрасывание монеты n раз. Каждому исходу опыта поставим в соответствие последовательность из n чисел последующему правилу: если при к- ом подбрасывании монеты выпал герб, то на к-ом месте последовательности фиксируем Г, а при выпадении решетки –Р. Например, последовательность (РР…РР) означает исход опыта, заключающийся в том, что каждый раз выпала решетка при n испытаниях. В частности, при n =3 принимаем ={ГГГ, ГГР, ГРГ, ГГГ, РРГ, РГР, ГРР, РРР}. При n больших значениях, число элементарных событий резко возрастает, оно равно .

4. Введем прямоугольную систему координат XOY. Пусть стрелок попадает непременно в какую-либо точку из круга радиуса 10 ед. с центром в начале координат. Тогда есть множество всех точек М(x,y) замкнутого этого круга.

Или можно записать в координатной форме так

.

Однако в реальном опыте кроме взаимоисключающих исходов можно указать много других случайных событий. Например, при бросании игральной кости можно говорить о выпадении четного числа очков. Это событие происходит только в том случае, когда происходит одно из трех элементарных событий

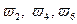. Представляется естественным каждое реальное событие в математической модели рассматривать как некоторое подмножество А множества .

В дальнейшем будет означать объединение двух множеств А и В, - пересечение этих множеств. Запись означает дополнение А к множеству В, т.е., оно состоит из элементов множества А, не принадлежащих В.

Итак, пусть - произвольное множество, а F – некоторый класс подмножеств множества . F называется алгеброй, если выполняются условия:

1. ;

2. Для любых : ;

3. Если .

Из последнего свойства следует, что .

Замечание 1. Нетрудно заметить, что в условии 2 достаточно требовать выполнения лишь одного из приведенных двух соотношений. Второе будет выполняться автоматически.

Замечание 2. Если -конечное множество, то система всех подмножеств будет также конечным множеством. Если множество состоит из n элементов, то число всех подмножеств равно .

Множество F называется -алгеброй или борелевской алгеброй, если из того, что следует .

Замечание 3. Достаточно выполнялось лишь одно из этих двух соотношений. Второе будет следствием равенства .

Элементы множества F будем называть событиями. Такой подход к понятию события удобен еще и тем, что благодаря ему понятия суммы и произведения событий, а также противоположного события приобретают естественный теоретико-множественный смысл. А именно, под суммой А+В событий А и В будем понимать объединение соответствующих подмножеств, под произведением АВ событий: A и B - пересечение тех же подмножеств, а под противоположным событием понимается событие, соответствующее подмножеству , то есть, дополнение к подмножеству А в .

Date: 2016-07-25; view: 380; Нарушение авторских прав