Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Локальная формула Муавра-Лапласа
|
|
Вернемся к биноминальному распределению. Производится n независимых испытаний, в каждом из которых событие А может появиться с постоянной вероятностью Р. Пусть случайная величина Х означает число появлений события А в n независимых испытаниях. Возможные значения таковы: 1,2,...,n; вероятности возможных значений вычисляются по формуле Бернулли
.
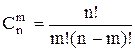Приведем без вывода числовые характеристики биноминального распределения:
.
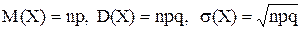Заметим, что при большом числе повторных испытаний n формула Бернулли приводит к громоздким вычислениям, т.е. в этом случае является неприемлемой в практических приложениях. Однако согласно следствию из теоремы Ляпунова биноминальное распределение при достаточно больших значениях n является асимптотически нормальным, т.е. приближенно можно считать нормальным распределением. Далее используя плотность распределения нормальной случайной величины 
,с учетом 
нетрудно получить следующую приближенную формулу
.
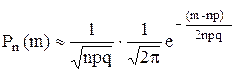Введем в рассмотрение функцию 
. Она является четной. Причем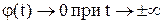 
. Значения функции 
обычно определяют по таблице значений этой функции. Последнюю приближенную формулу перепишем в виде
.
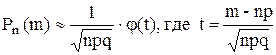Эта формула называется локальной формулой Муавра - Лапласа.
Замечание. Заметим, что вероятность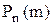 
принимает максимальное значение при m = np. При этом 
.
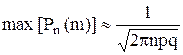Пример. Смесь состоит из хлопка и шерсти в пропорции 2:3. Определить вероятность того, что в случайном соединении из 120 волокон хлопковых волокон окажутся 30.
В нашем примере р = 0,4; q = 0,6; n =120; m =30. Поскольку число испытаний достаточно большое, поэтому целесообразно использовать локальную формулу Муавра-Лапласа. Сначала вычислим значение параметра t:
.
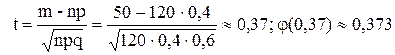Итак,
.
Date: 2016-07-25; view: 429; Нарушение авторских прав