Метод функционально законченных элементов

Во многих отраслях техники объекты состоят из некоторого конечного набора типовых конструктивных элементов. Каждый такой элемент имеет определенное функциональное назначение и выполняется в виде автономного объекта, завершенного в конст­руктивном отношении. При этом предусмотрена возможность его присоединения к другим типовым конструктивным элементам и создания на основе упорядоченной их совокупности некоторой интегрированной технической системы, обеспечивающей заданный процесс функционирования, отвечающий определенным тре­бованиям.

При наличии таких элементов они могут быть положены в основу структурирования объектов при их математическом описагнии. Это создает определенные преимущества при проектирова­нии. Структуру объекта составляют типовые элементы, имеющие соответствующие математические описания, которые используют­ся для получения полной математической модели технического объекта. Изменяя в процессе проектирования количественный и качественный состав элементов и варьируя их параметрами, мож­но получить в результате технический объект с высокими показа­телями качества и эффективности.

Метод структурирования технического объекта и построе­ния его математической модели в рассматриваемом случае назы­вают методом функционально законченных элементов. Этот ме­тод широко применяется при проектировании гидроприводов. Однако его можно использовать и в других областях техники.

Рассмотрим особенности этого метода на примере гидроме­ханических систем. Воспользуемся разработками, выполненными кандидатами технических наук Т.В. Пузановой и В.А. Широченко. В табл. 4.3 приведен предложенный ими набор структурных эле­ментов. Он обладает высокой гибкостью и позволяет составить динамическую модель любого гидропривода.

Математические модели функционально законченных эле­ментов можно получить различными методами, однако наиболее удобно воспользоваться уравнениями Лагранжа второго рода. В этом случае нет необходимости рассматривать взаимодействие элемента с другими элементами системы. Достаточно лишь соста­вить выражения для определения кинетической и потенциаль­ной энергий и диссипативной функции . Так как , и представляют собой квадратичные функции обобщенных коор­динат и обобщенных скоростей, то не возникает необходимости выбора направления координат или учета предполагаемого распо­ложения элемента в динамической модели. Воздействия на эле­мент, как внутренние, так и внешние, также не принимаются во внимание при построении его математической модели. Дело в том, что взаимодействия элементов будут учтены топологически­ми уравнениями при формировании математической модели системы, а для внешних воздействий составляются отдельные ма­тематические описания, входящие в библиотеку моделей воздей­ствий, которая, так же как и библиотека моделей элементов, ис­пользуется на стадии формирования полной модели системы.

Определив функции , и и используя уравнения Ла­гранжа второго рода, получают математическую модель элемента, которая в общем случае представляется выражением вида

, (4.55)

где — сила инерции элемента; — диссипативная сила эле­мента; — сила упругости элемента; F_B — сила взаимодействия данного элемента с другими элементами системы.

Для элементов вращательного движения вместо сил в урав­нение (4.55) будут входить соответствующие моменты

.

В табл. 4.3 указаны физические свойства, которыми наде­лены функционально законченные элементы, и даны математиче­ские описания этих свойств. В формулах приняты следующие обозначения параметров и фазовых переменных: 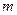, , — масса и моменты инерции соответствующих дискретных инерци­онных элементов; — площадь поперечного сечения гидромаги­страли; 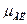, | — коэффициенты соответственно линейных и не­линейных потерь; — коэффициент вязкого трения; — плотность жидкости; — коэффициент расхода дросселя; , 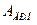— площади сечений соответственно постоянного и перемен­ного дросселей; — коэффициент местного сопротивления; , — коэффициенты гидромеханических потерь; 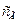— коэффици­ент жесткости упругого элемента, определяемый по формуле (3.66); 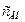— коэффициент жесткости возвратной пружины; — координата сосредоточенной массы, взаимодействующей с упру­гим элементом; — количество масс, взаимодействующих с дан­ным упругим элементом; , 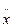— скорость и ускорение сосредото­ченной массы.

Значения 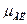и определяются по формулам:

; .

Обозначения параметров, входящих в эти формулы, даны в разделе 3.9.

Площадь сечения переменного дросселя зависит от факторов управления, где x — координата регулирующе­го органа дросселя; — управляющее давление; — время.

Обратный клапан рассматривается как безынерционный элемент переключения. В зависимости от направления скорости потока жидкости и разности давлений на его входе 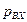и выходе он может находиться в открытом или закрытом состоянии.

Условие открытия при .

,

а условие закрытия при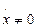

,

где — скорость потока жидкости в магистрали, в которой рас­положен обратный клапан; 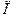— дискретная функция, характери­зующая условия работы клапана; 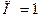, если клапан расположен в магистрали так, что пропускает жидкость только в положитель­ном направлении скорости потока; — в противном случае.

Если обратный клапан снабжен возвратной пружиной, то к добавляется слагаемое , где 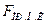— усилие пру­жины обратного клапана; — площадь перекрываемого клапа­ном отверстия — для шарикового или грибкового клапана, или площадь поверхности управляющего элемента — для золотнико­вого клапана.

Для построения математической модели системы необходи­мо использовать компонентные уравнения функционально закон­ченных элементов из табл. 4.3 и топологические уравнения, вы­ражающие условия равновесия потенциалов и непрерывности фазовых переменных типа потока. Топологические уравнения со­ставляются для узлов взаимодействия элементов. Как следует из табл. 4.3, каждый элемент представляет собой двухполюсник и содержит два узла, отмеченные цифрами 1 и 2. Исключение со­ставляет лишь безынерционный упругий элемент, отображающий упругие свойства газожидкостной смеси и трубопроводов, кото­рый содержит только один узел.

В гидромеханической системе взаимодействие функцио­нально законченных элементов осуществляется посредством рабо­чей жидкости, поэтому в качестве топологического уравнения ис­пользуется уравнение баланса расходов жидкости в узлах взаимодействия элементов, выражающее условие непрерывности фазовых координат:

, , (4.56)

где — расход жидкости -roэлемента, взаимодействующего с -м узлом; — количество элементов, взаимодействующих с этим узлом.

Давление жидкости в каждом узле взаимодействия одина­ково для всех функционально законченных элементов, примы­кающих к данному узлу.

Расход можно выразить через скорость потока жидкости 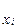и площадь его поперечного сечения . Тогда урав­нение непрерывности потока для - го узла принимает вид

(4.57)

Топологическое уравнение (4.57) эквивалентно уравнению позиционной связи

. (4.58)

Наличие позиционных связей системы приводит к избыточ­ности координат и переопределенности системы уравнений, по­этому избыточность желательно исключать.

Рассмотрим порядок ис­ключения избыточных коорди­нат на примерах. На рис. 4.8 приведен фрагмент динамиче­ской модели системы, отобра­жающей ветвление гидравличе­ской магистрали в точке 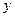. Участкигидромагистрали, при­мыкающие к узлу ветвления 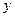, обладают инерционными, упру­гими и диссипативными свойст­вами. Эквивалентный упругий элемент с коэффициентом гид­равлической жесткости , ото­бражающий упругие свойства всех участков, располагается в узле ветвления. При малых объ­емах жидкости в участках и жестких трубопроводах упругими свойствами иногда пренебрега­ют и исключают из модели этот упругий элемент. Тогда коорди­наты всех инерционных элементов оказываются взаимосвязан­ными и число степеней свободы на единицу меньше общего числа координат.

Выберем в качестве зависимой координаты . Тогда в соот-вествии с уравнением связи (4.58) можно записать

,

где — число степеней свободы рассматриваемой подсистемы; , — независимая обобщенная координата; 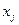— зависимая обоб­щенная координата (на рис. 4.8 ).

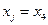Рис. 4.8. Фрагмент динамической модели гидравлической магистрали

В результате получаем уравнения связей между зависимыми 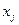и независимыми координатами системы

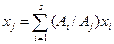, (4.59)

Предположим, что каждый элемент гидромеханической сис­темы обладает одновременно инерционными, диссипативными и упругими свойствами и подвергается внешнему воздействию . Движение такого элемента описывается дифференциальным урав­нением, структура которого имеет вид выражения (4.55).

Записав для всех элементов аналогичные уравнения и ис­ключив из них зависимые координаты и их производные, получа­ем систему дифференциальных уравнений в виде

, , (4.60)

где , , 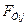— составляющие воздействия - го элемента с исключенной зависимой координатой ; на элемент системы с ко­ординатой — число исключаемых зависимых координат, равное числу уравнений связей.

Для фрагмента системы, изображенного на рис. 4.8 число степеней свободы , число связей , а математическая мо­дель его содержит 3 уравнения вида (4.60) и одно уравнение связи (4.59).

Систему уравнений (4.60) можно представить в виде

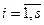, . (4.61)

Уравнения (4.61) в совокупности с уравнениями связей (4.59) представляют собой математическую модель динамической системы с sстепенями свободы. Решение этих уравнений позво­ляет определить все обобщенные координаты системы: независи­мые зависимые . При этом необходимо задать начальные условия , , .

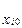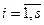Следует отметить, что не каждое уравнение системы (4.60) будет содержать составляющие, стоящие под знаком суммы. На­пример, если в подсистеме, приведенной на рис. 4.8 учесть упру­гие свойства газожидкостной смеси и трубопроводов, то коорди­наты всех инерционных элементов окажутся независимыми и уравнения будут иметь вид

,

Как следует из табл. 4.3, обобщенные координаты хiможно задать только тем функционально законченным элементам, кото­рые обладают инерционными свойствами. Математическое описа­ние остальных элементов должно осуществляться с использовани­ем обобщенных координат инерционных элементов.

Динамические модели гидроприводов представляют собой разветвленные разомкнутые цепи, а в системах автоматического управления — замкнутые одноконтурные или многоконтурные цепи. Точки ветвления цепей делят их на отдельные ветви, со­стоящие из некоторого набора последовательно соединенных функционально законченных элементов. Если в такую ветвь на­ряду с инерционными элементами входят также безынерционные, то описание последних дается с использованием обобщенных ко­ординат примыкающих инерционных элементов.

На рис. 4.9 даны ди­намические модели фраг­ментов ветвей. Узлы взаи­модействия входящих в них элементов обозначены . Фрагмент ветви на рис. 4.9, а включает три функционально закончен­ных элемента: участок гидромагистрали 1, посто­янный дроссель 6 и безы­нерционный упругий эле­мент 3 (обозначения элементов соответствуют их порядковым номерам, принятым в табл. 4.3).

Поскольку согласно принятым условиям при структурировании элемен­тов постоянный дроссель считается установленным в данный участок гидро­магистрали, а безынерци­онный упругий элемент примыкает к этому участ­ку, то состояние всех эле­ментов ветви определяется координатой сосредото­ченной массы жидкости в участке трубопровода 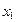. Используем координату 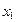и площадь поперечного се­чения участка трубопрово­да в моделях всех элементов ветви.

Рис. 4.9. Динамические модели ветвей гидроприводов, состоящих из взаимодействующих функционально законченных элементов

Решая совместно уравне­ния этих элементов, получаем дифференциальное уравнение рас­сматриваемой ветви

.

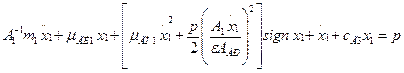Фрагмент схемы на рис. 4.9, б также содержит один эле­мент, обладающий инерционными свойствами (механический подвижный элемент 4). Остальные элементы безынерционные, по­этому математическое описание ветви можно составить, используя только одну независимую обобщенную координату .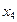

Выпишем уравнения всех компонентов ветви, обозначив их координаты номерами элементов:

;

;

,

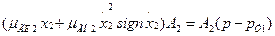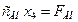где — давление жидкости в узле взаимодеиствия ; — усилие возвратной пружины.

Используя топологическое уравнение и ре­шая совместно компонентные уравнения, получаем дифференци­альное уравнение ветви

.

Для фрагмента схемы на рис. 4.9, в аналогичные выкладки приводят к уравнению ветви

Таким образом, несмотря на то, что в рассматриваемой вет­ви два инерционных элемента, получено одно дифференциальное уравнение с одной неизвестной 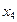, принятой в качестве независи­мой обобщенной координаты. Значение координаты 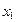определя­ется из уравнения связи: .

Если функционально законченные элементы, обладающие инерционными свойствами, разделены между собой упругим эле­ментом, их координаты оказываются независимыми. Так, дина­мическая модель ветви гидромеханической системы, представлен­ная на рис. 4.9, г, имеет две степени свободы и для ее математического описания необходимо использовать две незави­симые координаты 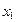и 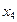. В результате получаем систему диф­ференциальных уравнений

При формировании математической модели объекта методом функционально законченных элементов система дифференциаль­ных уравнений (4.61) имеет не совсем обычный вид. В отдельные уравнения системы могут входить вторые производные одновре­менно нескольких обобщенных координат. В этой связи при необ­ходимости приведения их к нормальной форме Коши можно поступить следующим образом. Предполагаем искомыми неиз­вестными в системе уравнений (4.61) вторые производные незави­симых обобщенных координат и для их определения составля­ем систему неоднородных алгебраических уравнений вида

(4.62)

где — коэффициенты при искомых переменных 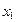; — функции возмущений, определяемые независимыми координата­ми и их первыми производными , а также внешними воздействиями на инерционные элементы системы , т.е.

, .

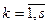Решив в общем виде систему уравнений (4.62) и введя обо­значение , получим следующую систему дифференци­альных уравнений в нормальной форме Коши:

(4.63)

где — давление, определяемое деформацией упругого элемента, расположенного - м узле взаимодействия элементов системы; 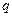— число узлов, в которых учитываются упругие свойства сис­темы.

Если упругим элементом является возвратная пружина, то ее усилие выражается через давление посредством соотношения , где — площадь рабочей поверхности механического подвижного элемента, с которым взаимодействует возвратная пружина.

Переменные и являются фазовыми координатами сис­темы гидропривода. При этом количество переменных типа пото­ка у, равно числу степеней свободы системы.

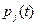Задавая начальные условия и и интегрируя систему уравнений (4.63), получают искомые функции скоростей движе­ния потоков жидкости и механических элементов гидропривода и давлений жидкости в узлах, в которых расположены упругие элементы.

Date: 2016-07-18; view: 804; Нарушение авторских прав