Матричная форма представления математической модели

Информация о математической модели технического объек­та, которую содержит орграф, может быть представлена в виде матрицы.

Сформируем матрицу размерности , где а — число строк, — число столбцов. В этой матрице каждому узлу оргра­фа, за исключением базового, соответствует строка, а каждой вет­ви — столбец. Единицами в матрице отметим наличие соединений между узлами и ветвями орграфа, а нулями — их отсутствие. На­правления сигналов в ветвях орграфа отобразим знаками единиц. Если сигнал направлен от узла, примем знак минус, а если к уз­лу — знак плюс.

Матрицу, построенную по изложенным правилам для дан­ного орграфа, называют матрицей инциденций.

В табл. 4.1 приведена матрица инциденций для техническо­го объекта, динамическая модель которого и орграф представлены на рис. 4.3, а в табл. 4.2 — для объекта, модели которого пред­ставлены на рис. 4.5.

Обозначим матрицу инциденций , ; , где — число узлов графа, за исключением базового; — сум­марное число ветвей орграфа — инерционных, диссипативных, упругих и источников внешних воздействий.

При составлении матрицы инциденций для объекта с источниками внешних воздействий типа потока в нее включают­ся не только узлы, отображающие сосредоточенные массы, но и узлы источников потоков, отмечаемые на орграфе и в матрице звездочкой и имеющие свою нумерацию. Кроме того, необходимо иметь в виду следующее. Каждый узел орграфа должен находить­ся в равновесии, что соответствует топологическому уравнению , где — потенциалы ветвей, инцидентных данному узлу. Выполнение этого условия для узла источника потока обеспечивается, если учесть реакцию внешней среды . Эта реакция представляет собой потенциал ветви орграфа, отображающей ис­точник потока. Поэтому источники потоков в матрице инциден­ций формально замещаются источниками реактивных потенциа­лов (см. табл. 4.2).

Матрицу инциденций можно представить состоящей из подматриц инерционных , диссипативных , упругих 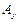вет­вей и подматрицы ветвей источников потенциалов :

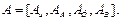
Из табл. 4.1 и 4.2 следует, что подматрица во всех слу­чаях единичная диагональная. В этой связи при составлении мат­рицы инциденций с целью упрощения обычно подматрицу опускают.

Рассмотрим подматрицу ветвей упругих компонентов 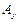для примера технического объекта на рис. 4.3 (табл. 4.1) и установим связь между нею и компонентными уравнениями упругих эле­ментов.

Компонентное уравнение упругого элемента механической вращательной системы имеет вид (см. табл. 3.1)

(4.1)

Для первого упругого элемента, согласно динамической мо­дели на рис. 4.3, , , следовательно, компонентное уравнение этого элемента

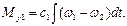(4.2)

Рассмотрим возможность получения этого же уравнения на основе матрицы инциденций. Примем во внимание, что состояние сосредоточенных масс, а следовательно, и отображающих их уз­лов графа, характеризуется фазовыми координатами типа потока . Учитывая это и используя столбец подматрицы 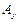, соответствующий данному упругому элементу, можно составить следующее выражение:

(4.3)

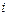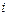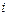где — фазовая координата типа потока (угловая скорость) -й сосредоточенной массы ( -гo узла орграфа); — инцидентор — элемент матрицы инциденций , характеризующий наличие или отсутствие соединения -й ветви орграфа с -м узлом и направле­ние сигнала в данной ветви; — число узлов орграфа.

Используя выражение (4.3), на основе матрицы инциден­ций, приведенной в табл. 4.1, получаем компонентное уравнение для первого упругого элемента, полностью совпадающее с уравне­нием (4.2).

Для второго упругого элемента получаем

(4.4)

а для третьего

. (4.5)

Сравнивая выражения (4.2), (4.4) и (4.5) и анализируя соот­ветствующие им столбцы подматрицы инциденций 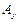ветвей уп­ругих элементов, легко обнаружить следующие закономерности. Если в столбце содержатся два ненулевых инцидентора, то упру­гий элемент соединяет между собой две сосредоточенные массы, т.е. осуществляет простое соединение. При наличии трех и более инциденторов (например, второй столбец подматрицы 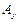в табл. 4.1) соединение сосредоточенных масс дифференциальное. Если инцидентор только один, то упругий элемент соединяет со­средоточенную массу с инерциальной системой отсчета. Такое со­единение называют реактивным, а упругий элемент, осуществ­ляющий это соединение, — реактивным упругим элементом.

Для получения компонентных уравнений инерционных эле­ментов по матрице инциденций используют выражение, которое составляется аналогично выражению (4.3):

, (4.6)

где 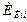— диагональный элемент подматрицы инциденций ветвей инерционных компонентов: для всех инерцион­ных компонентов, поэтому .

Компонентное уравнение диссипативного элемента

, (4.7)

где — элемент подматрицы инциденций ветвей диссипативных компонентов.

Таким образом, на основе матрицы инциденций можно по лучить все компонентные уравнения элементов технической системы и построить ее математическую модель в инвариант­ной форме. Следовательно, матрица инциденций несет ту же ин­формацию о системе, что и орграф или динамическая модель. По­этому ее можно рассматривать как функциональную математическую модель технического объекта в матричной форме.

Date: 2016-07-18; view: 634; Нарушение авторских прав