
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Графические формы представления математических моделей
|
|
В инженерной практике часто используют графические формы представления математических моделей. Для использования графических форм должно существовать правило однозначного соответствия условных изображений элементов графической модели и компонентов инвариантной математической модели.
Одной из форм отображения физических свойств технического объекта является динамическая модель. Графические изображения элементов динамической модели отождествляются с их компонентными уравнениями, а соединения элементов соответствуют топологическим уравнениям. Следовательно, динамическую модель можно рассматривать в качестве математической модели технического объекта в графической форме.
Структурирование динамической модели и идентификация ее элементов позволяют формализовать процесс составления математической модели технического объекта в инвариантной форме. Для этого удобно использовать графические формы моделей в виде графов и эквивалентных схем.
Граф представляет структурную математическую модель системы и отображает ее топологию, а эквивалентная схема — функциональную модель и отображает топологию и компонентный состав, так же как и динамическая модель. Если ввести обозначения ветвей графа, то он будет содержать ту же информацию, что и эквивалентная схема.
Компонентные уравнения элементов динамической модели представляют собой компоненты полной математической модели объекта. Уравнения инерционных, упругих и диссипативных элементов технических объектов различной физической природы приведены в табл. 3.1. Трансформаторные и фрикционные элементы отображают специфические особенности внутренних свойств системы и ее взаимодействия с внешней средой. Их математическое описание будет рассмотрено в главе 5.
Характеристики процессов функционирования объекта определяются не только его внутренними физическими свойствами, но и внешними воздействиями. Математические описания этих воздействий также являются компонентами математической модели. Воздействия представляют собой источники потенциалов  и источники потоков
и источники потоков 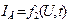 . При построении полной математической модели в инвариантной форме все компонентные уравнения посредством топологических уравнений сводят в единую систему. Это наиболее удобно осуществлять с помощью графов.
. При построении полной математической модели в инвариантной форме все компонентные уравнения посредством топологических уравнений сводят в единую систему. Это наиболее удобно осуществлять с помощью графов.
Граф представляет собой совокупность узлов (вершин) и соединяющих их ветвей (ребер). Такое же определение имеет и эквивалентная схема. Определение графа может быть записано в следующем виде: Г = (У, В, И), где У — множество узлов; В — множество ветвей; И — инцидентор — указатель способа соединения ветвей.
Ветви графа и эквивалентной схемы соответствуют компонентам математической модели. Они отображают математические описания инерционых, упругих и диссипативных элементов динамической модели и источников внешних воздействий.
Узлы, графа и эквивалентной схемы соответствуют узлам дискретизации непрерывных объектов в геометрическом пространстве, вводимым при переходе от моделей микроуровня к моделям макроуровня. При дискретизации системы методом сосредоточенных масс узлы дискретизации совпадают с сосредоточенными массами, представляемыми в динамической модели материальными точками или твердыми телами. Состояние технической системы и характер протекающих в ней процессов определяются фазовыми координатами узлов дискретизации. Эти координаты представляют собой потоковые переменные (например, в механической системе — скорости или геометрические координаты).
Сосредоточенные массы динамической модели обладают дуальными свойствами: они отображают инерционные свойства технической системы и одновременно являются носителями информации о ее состоянии. Последнее выражается в том, что систему фазовых координат динамической модели связывают непосредственно с сосредоточенными массами.
Граф и эквивалентная схема позволяют эти свойства сосредоточенных масс дифференцировать более четко: инерционные свойства отображаются ветвями, а носители информации о состоянии технической системы — узлами. В результате каждая сосредоточенная масса отображается узлом графа или эквивалентной схемы, а ее физические свойства — ветвью инерционного элемента.
Узлы графа обозначают точками, а ветви линиями (рис. 4.1). Узлам присваивают номера сосредоточенных
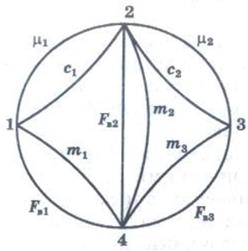
Рис. 4.1. Пример графа механической системы
масс, а ветвям дают обозначения параметров отождествляемых ими элементов динамической модели или обозначения источников внешних воздействий (источник потенциалов UB или источник потоков /в). Один из узлов графа и эквивалентной схемы отображает инерциальную систему отсчета фазовых координат типа потока. Его называют базовым узлом (или базой) и ему присваивается нулевой номер.
Для обозначения различных ветвей эквивалентной схемы рекомендуется применять графические изображения, показанные на рис. 4.2. Ветви эквивалентной схемы и графа, отображающие внутренние свойства технического объекта, можно именовать так же, как и соответствующие им элементы динамической модели, т.е. инерционные, упругие и диссипативные. Поскольку эти ветви суть компоненты математической модели в графической форме, то и компоненты имеют те же наименования, что и ветви.
На эквивалентных схемах и графах применяют обозначения параметров элементов и источников внешних воздействий соответственно виду моделируемой технической системы (см. табл. 3.2 и 3.3). На рис. 4.2 использованы обозначения для механической поступательной системы.
Рассмотрим особенности построения эквивалентной схемы и графа на примере механической вращательной системы, динамическая модель которой приведена на рис. 4.3, а. Модель отображает инерционные, упругие и диссипативные элементы системы и внешние воздействия на нее. Элементы динамической модели обозначаются на схеме их параметрами с цифровыми индексами, соответствующими порядковым номерам элементов: Jt — моменты инерции вращающихся твердых тел (сосредоточенных масс); Cj, — коэффициенты же- сткостей и сопротивлений соответственно упругих и диссипативных элементов. На динамической модели необходимо также отобразить внешние воздействия на технический объект. Источники потенциалов воздействуют непосредственно на сосредоточен
ные массы, а источники потоков со — на упругие и диссипативные элементы. Рассматриваемый объект подвержен воздействиям только источников потенциалов 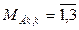 .
.

Рис. 4.2. Обозначение ветвей эквивалентной схемы: а — инерционной; б — диссипативной; в — упругой; г — источника потенциала; д — источника потока
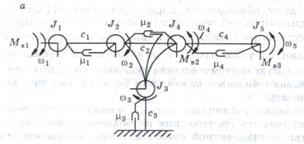
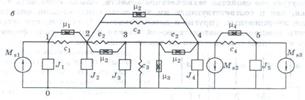

Рис. 4.3. Динамическая модель (а), эквивалентная схема (б) и орграф (в) механической вращательной системы
Источники воздействий могут сообщать энергию объекту или отводить ее от объекта. Для отображения этого на динамической модели должны быть указаны положительные направления фазовых координат типа потока  (или
(или 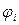 ), характеризующих состояния сосредоточенных масс, а также направления потоков энергии, сообщаемой объекту источниками внешних воздействий
), характеризующих состояния сосредоточенных масс, а также направления потоков энергии, сообщаемой объекту источниками внешних воздействий 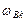 и
и 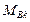 . Если энергия источника потенциала подводится к объекту, то направления
. Если энергия источника потенциала подводится к объекту, то направления  и
и 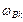 совпадают, а если отводится (т.е. вместо источника имеет место сток), то их направления противоположны. В рассматриваемом примере вращающий момент
совпадают, а если отводится (т.е. вместо источника имеет место сток), то их направления противоположны. В рассматриваемом примере вращающий момент  является движущим, увеличивающим энергию объекта (к объекту подводится энергия двигателя), поэтому направления
является движущим, увеличивающим энергию объекта (к объекту подводится энергия двигателя), поэтому направления  и
и 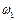 совпадают. Вращающие моменты
совпадают. Вращающие моменты 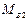 и
и  характеризуют сопротивления внешней среды движению объекта, на преодоление которых затрачивается его энергия. В этой связи направления
характеризуют сопротивления внешней среды движению объекта, на преодоление которых затрачивается его энергия. В этой связи направления 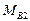
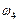 , а также
, а также  и
и 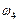 не совпадают.
не совпадают.
Потенциалы упругих  и диссипативных
и диссипативных 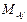 элементов, характеризующие их взаимодействие с другими элементами системы, являются внутренними воздействиями и на динамической модели не изображаются.
элементов, характеризующие их взаимодействие с другими элементами системы, являются внутренними воздействиями и на динамической модели не изображаются.
Следует обратить внимание на то, что функции источников внешних воздействий типа потока 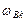 и типа потенциала
и типа потенциала 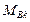 обозначаются такими же символами, как и фазовые координаты типа потока
обозначаются такими же символами, как и фазовые координаты типа потока  ; и типа потенциала
; и типа потенциала  ,
, 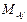 моделируемого технического объекта. Чтобы их различать в динамических моделях, в обозначениях внешних воздействий вводится индекс «в».
моделируемого технического объекта. Чтобы их различать в динамических моделях, в обозначениях внешних воздействий вводится индекс «в».
Если один и тот же упругий элемент соединяет между собой более двух сосредоточенных масс, т.е. образует кольцевое соединение (например, элемент с2 на рис. 4.3, а), то такое соединение называется дифференциальным, а если кольцевое соединение сосредоточенных масс осуществляется различными упругими элементами, то его называют гираторным. Это же относится и к диссипативным элементам.
В случае дифференциального соединения следует иметь в виду, что все сосредоточенные массы, входящие в соединение, взаимодействуют с одним и тем же упругим и диссипативным элементами, что и отражено на схеме рис. 4.3, а.
При моделировании сложных технических объектов графические изображения диссипативных элементов на динамических моделях могут значительно усложнить чертеж (схему). Но если диссипативные элементы расположены в модели параллельно упругим элементам (что характерно для большинства механических систем), тогда их графические изображения можно исключить, а вместо них наличие диссипативных элементов отметить записью параметров 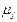 рядом с параметрами
рядом с параметрами 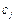 упругих элементов (при этом обозначения
упругих элементов (при этом обозначения 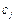 и
и 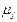 должны разделяться между собой запятой). Это допущение будет использоваться в дальнейшем в динамических моделях вращательных механических систем (например, на рис. 4.6).
должны разделяться между собой запятой). Это допущение будет использоваться в дальнейшем в динамических моделях вращательных механических систем (например, на рис. 4.6).
Построение эквивалентной схемы (рис. 4.3, б) начинают с инерционных ветвей, которые располагают вертикально. Эти ветви соединяют узлы, отождествляющие сосредоточенные массы системы, с базовым узлом, соответствующим инерциальной системе отсчета фазовых координат типа потока. Ветви упругих и диссипативных компонентов соединяют между собой взаимодействующие узлы, в соответствии с динамической моделью. Ветви источников потенциалов связывают узлы, к которым они приложены, с базой.
Граф является аналогом эквивалентной схемы и структура его аналогична (рис. 4.3, в). Если обозначить направления сигналов в ветвях графа, то получим ориентированный граф (орграф). Направления сигналов в ветвях графа изображают стрелками.
В ветвях источников внешних воздействий сигналы направляют от базы к узлу, если энергия подводится к узлу и источник обеспечивает возрастание потоковой переменной узла. В случае источника потенциала подвод энергии осуществляется при условии совпадения направлений 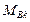 и
и  . При отводе энергии на преодоление сопротивлений направления
. При отводе энергии на преодоление сопротивлений направления 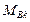 и
и  , противоположны, поэтому направление сигнала в ветви источника — от узла к базе. Направление сигнала в ветви источника потока определяется аналогично, в зависимости от того, подводится энергия к техническому объекту от внешней среды или отводится.
, противоположны, поэтому направление сигнала в ветви источника — от узла к базе. Направление сигнала в ветви источника потока определяется аналогично, в зависимости от того, подводится энергия к техническому объекту от внешней среды или отводится.
Во всех ветвях инерционных компонентов направления сигналов от узлов к базе. Такое направление характеризует затраты энергии источников на увеличение кинетической энергии инерционных элементов. В любых других ветвях, соединяющих узлы с базой, кроме ветвей источников, сигналы всегда направлены к базе.
В ветвях упругих компонентов стрелки указывают направление передачи энергии от источников к потребителям. Если ветви диссипативных компонентов параллельны ветвям упругих компонентов, то направления сигналов в них одинаковые.
Однако встречаются случаи, когда нельзя однозначно указать направление передачи энергии в некоторых ветвях графа. Это характерно для систем с дифференциальным соединением сосредоточенных масс. В рассматриваемом примере сосредоточенные массы с моментами инерции J2, J3 и J4 соединены упругим элементом с коэффициентом жесткости 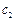 и диссипативным элементом с коэффициентом сопротивления
и диссипативным элементом с коэффициентом сопротивления  . В результате на эквивалентной схеме узлы 2, 3 и 4 связаны между собой одними и теми же упругими и диссипативными ветвями
. В результате на эквивалентной схеме узлы 2, 3 и 4 связаны между собой одними и теми же упругими и диссипативными ветвями 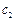 и
и  . Энергия передается от узла 2 к узлам 3 и 4, но направление передачи энергии между узлами 3 и 4 априори установить нельзя.
. Энергия передается от узла 2 к узлам 3 и 4, но направление передачи энергии между узлами 3 и 4 априори установить нельзя.
Орграф, в отличие от эквивалентной схемы, содержит только ориентированные ветви. В этой связи упругая и диссипа-тивная ветви 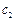 и
и  эквивалентной схемы, соединяющие узлы 3 и 4, на орграфе отсутствуют. Вместе с тем следует отметить, что отображать соединение этих узлов на орграфе нет необходимости. Орграф вполне определенно иллюстрирует взаимодействие всех трех узлов и отражает распределение энергии между узлами 3 и 4, передаваемой к ним через упругий и диссипативный элементы
эквивалентной схемы, соединяющие узлы 3 и 4, на орграфе отсутствуют. Вместе с тем следует отметить, что отображать соединение этих узлов на орграфе нет необходимости. Орграф вполне определенно иллюстрирует взаимодействие всех трех узлов и отражает распределение энергии между узлами 3 и 4, передаваемой к ним через упругий и диссипативный элементы 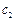 и
и  от узла 2.
от узла 2.
При гираторном соединении (рис. 4.4, а) каждая пара сосредоточенных масс соединена своими упругими и диссипативны- ми элементами, поэтому все они должны быть отображены на орграфе соответствующими ветвями с указанием направлений в них сигналов (рис. 4.4, в). Здесь также определить направление сигнала в одной из ветвей может оказаться затруднительным. В этом случае принимают произвольное направление.



Рис. 4.4. Динамическая модель (а), эквивалентная схема (б) и орграф (в) технического объекта с гираторным соединением сосредоточенных масс
Пример 4.1. Составить графические формы математических моделей для анализа колебаний кузова автомобиля, обусловленных неровностями дороги.
На рис. 4.5, а приведена одна из возможных динамических моделей (см. также рис. 3.1, в). Твердые тела массами  и
и 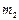 (кузов и колеса автомобиля) совершают поступательные движения. Фазовые переменные типа потока в механической поступательной системе - скорости
(кузов и колеса автомобиля) совершают поступательные движения. Фазовые переменные типа потока в механической поступательной системе - скорости 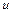 , а типа потенциала - силы F. На систему наряду с источниками потенциалов
, а типа потенциала - силы F. На систему наряду с источниками потенциалов  и
и  действует источник потока, описываемый функцией
действует источник потока, описываемый функцией  . Источник потока отображает кинематическое воздействие внешней среды - неровностей дороги. Характеристикой этого источника является функция изменения скорости вертикального перемещения опорной точки D, определяемая выражением
. Источник потока отображает кинематическое воздействие внешней среды - неровностей дороги. Характеристикой этого источника является функция изменения скорости вертикального перемещения опорной точки D, определяемая выражением 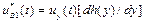 , где
, где  - скорость движения автомобиля вдоль оси у: h(y) — функция микропрофиля поверхности дороги. Потенциалы внешних воздействий
- скорость движения автомобиля вдоль оси у: h(y) — функция микропрофиля поверхности дороги. Потенциалы внешних воздействий  и
и  представляют собой силы тяжести соответственно кузова и колес автомобиля. Эти силы постоянны и их обычно не включают в модель при анализе малых колебаний. Однако при определении усилий в упругих элементах их необходимо учитывать. Кроме того, взаимные перемещения кузова и колес автомобиля ограничены направляющими устройствами подвески, а величины допускаемых перемещений зависят от значений усилий
представляют собой силы тяжести соответственно кузова и колес автомобиля. Эти силы постоянны и их обычно не включают в модель при анализе малых колебаний. Однако при определении усилий в упругих элементах их необходимо учитывать. Кроме того, взаимные перемещения кузова и колес автомобиля ограничены направляющими устройствами подвески, а величины допускаемых перемещений зависят от значений усилий  и
и  .
.
При наличии источников потоков взаимодействие технического объекта с внешней средой осуществляется посредством упругих и (или) диссипативных элементов. В эквивалентной схеме и орграфе это приводит к возникновению дополнительных узлов, определяющих соединения ветвей упругих и диссипативных компонентов с ветвями источников потоков.
На рис. 4.5, б построена эквивалентная схема, а на рис. 4.5, в орграф рассматриваемой системы. Узлы 1 и 2 отображают сосредоточенные массы, а узел
1* - внешнюю среду, генерирующую воздействие типа потока 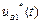 , передаваемое на упругий и диссипативный элементы
, передаваемое на упругий и диссипативный элементы 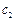 и
и  колес автомобиля. Узлы источников потоков имеют свою нумерацию и обозначаются звездочкой.
колес автомобиля. Узлы источников потоков имеют свою нумерацию и обозначаются звездочкой.
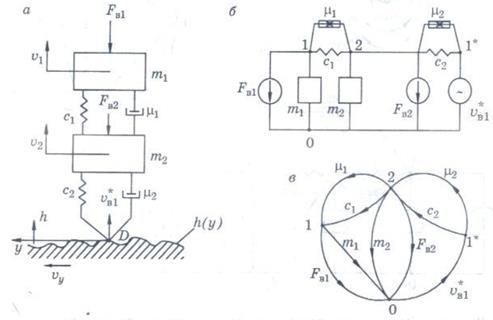
Рис. 4.5. Динамическая модель (а), эквивалентная схема (б) и орграф (в) механической поступательной системы с источником внешнего воздействия типа потока
Таким образом, орграф позволяет идентифицировать структуру и физические свойства моделируемой технической системы и представляет собой ее математическую модель в графической форме. Использование орграфа дает возможность формализовать процесс составления полной математической модели объекта в инвариантной форме, т.е. получить систему обыкновенных дифференциальных уравнений, описывающих процесс функционирования технического объекта.
Эквивалентную схему применяют обычно лишь при предметном моделировании, когда необходимо иметь схему замещения для построения эквивалентной динамической модели на элементах иной физической природы. При математическом моделировании технических систем ограничиваются использованием орграфов.
Date: 2016-07-18; view: 2457; Нарушение авторских прав