Определение параметров элементов динамических моделей технических объектов

Механическая система. Параметры инерционных элемен-тов — массы т и моменты инерции и упругих элементов — коэффициенты жесткости с определяют по известным формулам теоретической механики.

Параметры диссипативных элементов — коэффициенты

сопротивлений можно найти, используя априорную информа­цию об относительных коэффициентах затухания колебаний 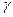(коэффициентах апериодичности). Значения 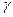обусловлены трени­ем в конструктивных элементах технической системы, возни­кающим в результате их деформации и взаимных микропереме­щений сочлененных деталей. Влияние трения в материале для металлических конструкций обычно во много раз меньше, чем трения в сочленениях деталей. В деталях, изготовленных из по­лимеров (резина, пластмасса и др.), трение значительно больнее, чем в аналогичных металлических деталях (значение 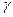примерно

в 100 раз выше). В зависимости от конструктивного исполнения технической системы упругие элементы ее динамической модели могут отображать как отдельные сплошные (неделимые) детали, обладающие сравнительно небольшой жесткостью (например, пружины, длинные валы), так и целый ряд сочлененных деталей. В этой связи величина 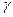колеблется в значительных пределах:

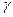= 0,03...1,0. Для гашения колебаний применяют специальные

демпфирующие элементы (резиновые муфты, гидравлические амортизаторы и др.), позволяющие значительно увеличить 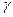и

снизить амплитуды колебаний.

Коэффициент сопротивления 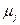- го диссипативного эле­мента механической системы зависит не только от , но и от па­раметров элементов динамической модели, непосредственно при­мыкающих к данному диссипативному элементу. При определении значений 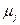используют парциальные системы.

Парциальной системой называется частичная одночастотная подсистема, выделяемая из динамической модели техническо­го объекта. Она имеет только одну частоту собственных колеба­ний, называемую собственной парциальной частотой. На рис. 3.3 показаны динамические модели парциальных систем объектов механической природы с вращательным движением со­средоточенных масс. Особенность структуры парциальной систе­мы состоит в том, что она содержит один базовый элемент и не- которое множество взаимодействующих с ним элементов с иными физическими свойствами по сравнению с базовым элементом. На рис. 3.3, а, в, д базовым является инерционный элемент с пара­метром , а на рис. 3.3, б, г, е — упругий элемент с параметром

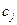. Парциальные системы, показанные на рис. 3.3, а, б называют

простыми, а на рис. 3.3, в — е — сложными.

Рис. 3.3. Динамические модели парциальных систем:

а, в, д — с инерционным базовым элементом;

б, г, е — с упругим базовым элементом

Собственная парциальная частота определяется без учета диссипативных элементов. Это частота свободных незатухающих колебаний парциальной системы. Для системы с инерционным базовым элементом она вычисляется по формуле

(3.50)

а для системы с упругим базовым элементом

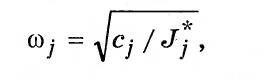
(3.51)

где 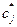— приведенный к -му инерционному базовому элементу коэффициент жесткости -го упругого элемента; К — количество упругих элементов, входящих в парциальную систему; 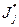— па­раметр эквивалентного приведенного инерционного элемента, ки­нетическая энергия которого равна сумме кинетических энергий всех инерционных элементов парциальной системы.

Рассмотрим вначале парциальные системы с инерционным базовым элементом (рис. 3.3, а, в, д). Необходимость определения параметра 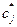возникает при наличии в парциальной системе трансформаторных элементов, что характерно для системы на рис. 3.3, д. Значение параметра 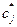определяется из условия ра­венства потенциальных энергий исходного упругого элемента с параметром и приведенного упругого элемента с параметром

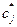. Если упругий элемент расположен на входе инерционного элемента, как на рис. 3.3, д, то приведенный коэффициент

жесткости этого элемента получают умножением на квадрат передаточного числа 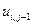трансформаторного элемента

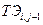, а если на выходе, то делением:

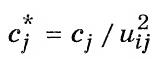
Вход и выход базового элемента определяются по на­правлению передаваемого через динамическую систему потока энергии. Передаточное число трансформаторного элемента равно отношению скорости на его входе к скорости на выходе.

При отсутствии трансформаторных элементов (рис. 3.3, а, в)

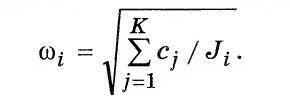(3.50а)

Рассмотрим определение параметра 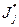для парциальных систем с упругим базовым элементом. При отсутствии трансфор­маторных элементов (рис. 3.3, б, г)

где N — количество инерционных элементов, входящих в парци­альную систему.

Если же парциальная система содержит трансформаторные

элементы (рис. 3.3, е), то в формулу (3.52) вместо необходимо подставлять приведенные к упругому базовому элементу моменты инерции 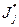. Значение 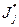определяется из условия равенства ки­нетических энергий исходного инерционного элемента с параметром и приведенного с параметром 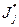. Если инерционный эле­мент расположен на входе базового упругого элемента, то умножают на квадрат передаточного числа трансформаторного элемента, а если на выходе, тогда делят. Для парциальной систе­мы на рис. 3.3, е

Пусть энергия в системе на рис. 3.4, а передается от массы 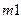к массе , а на рис. 3.4, б от массы к массе . Обе систе­мы имеют по два трансформаторных элемента ТЭ1 и ТЭ2.

Рис. 3.4. Парциальные системы с трансформаторными элементами ТЭ1 и ТЭ₂: а — поступательная, б — вращательная

В поступательной системе на рис. 3.4, а трансформаторные элементы отображают рычажные передачи. Передаточное число ТЭ1 найдем через отношение скоростей точек Л и Б, а передаточ­ное число ТЭ2 — скоростей точек и Е:

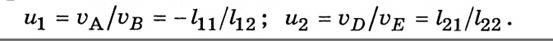
Так как ТЭ1 расположен на входе в упругий элемент, а ТЭ2 — на его выходе, то значение т* вычислим по формуле

Аналогично определяется для парциальной системы на рис. 3.5, б:

где и и₂ — передаточные числа ТЭ1 и ТЭ2, отображающие зуб­чатые передачи: — числа зубьев передач.

При определении параметров диссипативных элементов используются парциальные системы с упругим базовым элемен­том. Значение 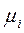определяется по формуле

(3.53)

При поступательном движении твердых тел в формулы (3.50) — (3.53) вместо моментов инерции и 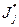подставляют значения масс и . На рис. 3.5 показан пример выделения парциальной системы с упругим базовым элементом 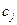из дина­мической модели механической поступательной системы.

Парциальные системы с инерционным базовым элементом используют при упрощении динамических моделей технических объектов.

Date: 2016-07-18; view: 526; Нарушение авторских прав