Компонентные и топологические уравнения гидравлической системы

В гидравлической системе фазовыми переменными типа потока являются расходы (, м³/с, а типа потенциала — давле­ния р, Н/м² (Па).

При выводе компонентных уравнений используем уравне­ния Эйлера, Навье—Стокса и Гука, полученные для одномерной системы с распределенными параметрами.

Для перехода к модели с сосредоточенными параметрами осуществим аппроксимацию моделей микроуровня путем замены частных производных фазовых переменных по пространственным координатам отношениями конечных разностей.

Уравнение Эйлера для трубопровода постоянного сечения

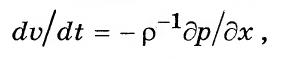(3.16)

где V — скорость потока жидкости в трубопроводе; р — плотность жидкости; х — геометрическая координата.

Разделим трубопровод на ряд участков длиной I и заменим частную производную др/дх отношением конечной разности

(3.17) (3.17)

где Р1, Р2 — давления в узлах дискретизации 1 и 2, т.е. на грани­цах выделенных участков трубопровода.

Здесь учтено, что градиент давления вдоль трубопровода 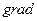р = др/дх отрицателен (давление падает по мере удаления от

источника).

Расход жидкости в трубопроводе выразим через скорость потока :

(3.18) (3.18)

где А — площадь поперечного сечения трубопровода.

Подставим значения др/дх из (3.17) и из (3.18) в уравне­ние (3.16) и найдем выражение для определения р:

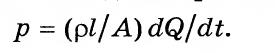
Введем обозначение

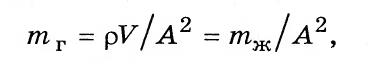(3.19) (3.19)

где т _г — коэффициент массы, кг/м⁴; V — объем жидкости в вы­деленном участке трубопровода длиной I: У=А ; т_ж — масса жид­кости в этом участке.

С учетом (3.19) уравнение Эйлера (3.16) после дискретиза­ции приводится к виду

(3.20)

Сопоставляя (3.20) с выражением (3.1), приходим к выводу, что уравнение Эйлера отображает только инерционные свойст­ва жидкости.

Рассмотрим линеаризованное уравнение Навье – Стокса

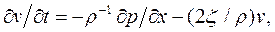(3.21)

где - коэффициент линеаризованного вязкого трения жидкости.

Учитывая выражения (3.17) и (3.18), получаем

Введем обозначение

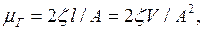(3.22)

где - коэффициент гидравлического сопротивления,

С учетом выражений (3.19) и (3.22) уравнение Навье – Стокса после дискретизации приводиться к виду

(3.23)

Из выражения (3.23) следует, что уравнение Навье – Стокса отображает инерционные и диссипативные свойства жидкости. В этом случа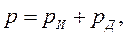е где - величина потерь давления на преодоление трения при движении потока жидкости в трубопроводе, а - затраты давления на разгон жидкости. Полагая и аддитивными величинами, выделим инерционный и диссипативный элементы участка трубопровода. Компонентное уравнение инерционного элемента соответствует выражению (3.20), а диссипативного элемента имеет вид

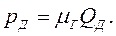(3.24)

Уравнение Гука

(3.25)

позволяет учесть упругие свойства жидкости. Выразим скорость потока v через расход Q по формуле (3.18). Тогда 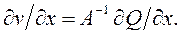Заменим 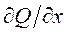отношением конечной разности

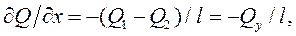(3.26)

где 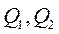- расходы в узлах дискретизации трубопровода 1 и 2; 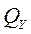- изменение расхода, обусловленное сжимаемостью жидкости.

В выражении (3.26) учтено, что при возрастании давления происходит увеличение объемной деформации жидкости и величина расхода жидкости при удалении от источника уменьшается.

На основе уравнения (3.25) с учетом выражения (3.26) найдем выражение для определения давления упругого элемента, полагая Е не зависящим от р:

(3.27)

Введем обозначение

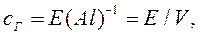(3.28)

где 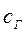- коэффициент гидравлической жесткости, ; Е – модуль объемной упругости жидкости, .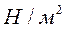

В результате получаем компонентное уравнение упругого элемента гидравлической системы

(3.29)

Фазовые переменные , , представляют собой внутренние потенциалы исследуемой гидравлической системы, характеризующие взаимодействие выделенных дискретных элементов и определяющие потери давления источника на преодоление сил инерции жидкости и сообщение ей кинетической энергии, на деформацию жидкости и изменение ее потенциальной энергии, а также на преодоление сил внутреннего трения жидкости.

Коэффициенты , 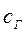и являются параметрами соответственно инерционных, упругих и диссипативных элементов гидравлической системы.

Топологические уравнения имеют вид

; (3. 30)

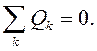(3.31)

Первое уравнение выражает условие равновесия потенциалов, действующих на сосредоточенные массы, а второе – условие непрерывности потоков жидкости.

Date: 2016-07-18; view: 599; Нарушение авторских прав