Узловой метод формирования математической модели

Для формирования полной математической модели техниче­ского объекта на основе компонентных и топологических уравне­ний наиболее широкое применение получил узловой метод.

Напомним, что компонентные уравнения описывают физи­ческие свойства простых элементов, устанавливая соотношения между фазовыми переменными типа потока и типа потенциала, характеризующими состояния элементов. Топологические уравне­ния описывают условия равновесия и непрерывности фазовых пе­ременных.

Используем обозначения фазовых переменных и парамет­ров, применяемые для механической поступательной системы, и выпишем компонентные и топологические уравнения в этих обо­значениях.

Принимая во внимание, что фазовые переменные системы 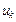и 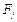составляют некоторые множества, запишем компонентные уравнения элементов системы в матричной форме:

уравнения инерционных элементов

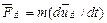; (4.8)

уравнения диссипативных элементов

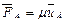; (4.9)

уравнения упругих элементов

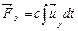, (4.10)

Где 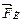, , 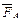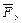— векторы потенциалов соответственно инерци­онных, диссипативных и упругих 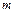элементов; , , — диагональные матрицы параметров этих же элементов; 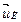, , 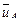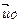— векторы фазовых переменных типа потока соответствующих эле­ментов.

Топологические уравнения механической поступательной системы:

уравнение равновесия потенциалов ветвей орграфа, инци­дентных 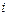-му узлу,

, ;

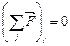уравнение непрерывности фазовых переменных типа потока 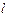-й ветви орграфа

, ,

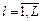Где — число узлов орграфа, за исключением базового; — чис­ло ветвей.

Используя матрицу инциденций, топологические уравнения можно записать в матричной форме

; (4.11)

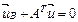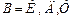, , (4.12)

где — матрица инциденций; — транспонированная матрица ; — вектор потенциалов ветвей; , 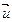— векторы потоковых переменных соответственно ветвей и узлов графа.

Элемент вектора определяется по формуле:

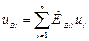, (4.13)

где — элемент матрицы инциденций, характеризующий ин­цидентность 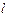-Й ветви орграфа 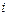-му узлу.

Основные положения узлового метода:

1) в качестве базисных координат используются узловые потоковые переменные 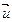, характеризующие состояния узлов графа;

2) исходным топологическим уравнением системы явля­ется уравнение равновесия потенциалов ветвей в узлах графа (4.11), выражающее принцип Даламбера.

Вектор потенциалов системы представим состоящим из подвекторов потенциалов компонентов — инерционных 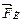, диссипативных , упругих 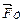и источников внешних воздействий :

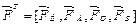. (4.14)

Аналогично можно представить матрицу инциденций, со­стоящей из соответствующих подматриц:

(4.15)

Используя разложения (4.14) и (4.15), приведем уравнение равновесия (4.11) к виду

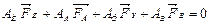. (4.16)

Подставим значения потенциалов ветвей из уравнений (4.8) — (4.10) в равенство (4.16):

.

Учитывая топологическое уравнение (4.12), фазовые пере­менные 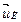, , 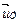можно выразить через узловые потоковые пере­менные 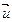. В результате получаем матричное уравнение, описы­вающее алгоритм формирования математической модели узловым методом,

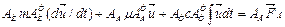. (4.17)

Изложенный классический вариант узлового метода при­водит к системе интегродифференциальных уравнений (4.17). Такой вид уравнений неудобен для анализа процесса функциони­рования объекта. Как уже упоминалось, наиболее предпочтитель­ной формой математической модели при использовании числен­ных методов является система дифференциальных уравнений в нормальной форме Коши. Однако отмеченный недостаток узлово­го метода можно легко устранить.

Преобразование интегродифференциальных уравнений (4.17) к нормальной форме можно осуществить путем расширения координатного базиса. Введем функции потенциалов упругих компонентов в состав базисных координат. Эти функции пред­ставляются выражением

. (4.18)

Подставим значение в уравнение (4.17) и разрешим его относительно производной . Определим производную повремени от вектор-функции . Полученные выражения сведем в

единую систему уравнений. В результате получим систему обык­новенных дифференциальных уравнений в нормальной форме Коши

(4.19)

В уравнениях (4.19) базисными координатами являются фа­зовые переменные 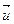и 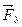. Базисными координатами называют совокупность неизвестных переменных в уравнениях, описы­вающих функционирование динамической системы.

Для системы с источниками внешних воздействий типа по­тенциала потоковые фазовые переменные vхарактеризуют со­стояние сосредоточенных масс и являются независимыми коор­динатами, а их количество равно числу степеней свободы системы. При этом число узлов орграфа п (за вычетом базового) равно числу сосредоточенных масс.

Орграф объекта с источниками внешних воздействий типа потока включает дополнительные узлы, отображающие внешнюю среду, генерирующую эти воздействия. Их называют узлами ис­точников потоков. Такие узлы имеют свою отдельную нумера­цию и отмечаются на орграфе звездочками (рис. 4.5, в). Узлы ис­точников потоков характеризуются двойственными (дуальными)

свойствами, отображаемыми двумя различными функциями 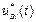и . Функция 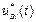характеризует внешнее воздействие ти­па потока, возникающее в результате взаимодействия объекта с внешней средой. Функция характеризует состояние 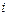-й со­средоточенной массы, отображаемое потоковой переменной . В этой связи переменная входит в координатный базис системы

уравнений (4.19), а функция 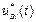— в число внешних воздейст­вий. Но поскольку сосредоточенные массы, отображаемые узлами источников потоков, принадлежат внешней среде, с которой свя­зана инерциальная система отсчета фазовых координат типа по­тока, то 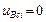и . В результате дифференциальные уравнения относительно производных фазовых координат превращаются в алгебраические выражения, используемые для вычисления реактивных потенциалов внешней среды. Неза­висимыми координатами системы являются только фазовые пе­ременные типа потока v, характеризующие состояния сосредо­точенных масс технической системы. Эти массы отображают­ся на орграфе узлами с порядковыми номерами без индексов. Их количество равно числу степеней свободы системы.

Подматрица инерционных ветвей орграфа , как отмеча­лось, является единичной матрицей. Порядок этой матрицы для объекта с источниками потенциалов равен числу степеней свобо­ды системы , а для объектов с источниками потоков ее порядок , где — количество источников потоков. Однако во всех случаях эта матрица квадратная. Такой же порядок имеет и диа­гональная матрица параметров инерционных элементов 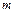. Для объектов с источниками потоков в состав матрицы 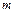входят также элементы , являющиеся параметрами инерционности внешней среды. При моделировании технических объектов инер­ционность внешней среды полагают бесконечно большой, поэтому включение параметров в состав матрицы т необходимо рас­сматривать как формальный прием обеспечения необходимой ее размерности.

Так как матрицы , и 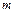одного и того же порядка , то матричное произведение в первом уравнении системы (4.19) . С учетом этого уравнения (4.19) можно записать в виде:

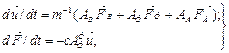(4.20)

где 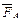— вектор потенциалов диссипативных компонентов:

. (4.21)

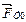Для решения системы обыкновенных дифференциальных уравнений (4.20) необходимо задать начальные условия и при .

Проанализируем структуру системы уравнений (4.20). Пер­вое матричное уравнение системы (4.20) выражает принцип Даламбера, а второе является компонентным уравнением упругих элементов. Уравнение (4.21) также матричное и представляет собой компонентное уравнение диссипативных элементов.

В системе уравнений (4.20) число неизвестных функци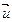й и равно числу дифференциальных уравнений. Следовательно, узловой метод позволяет избежать избыточности фазовых коорди­нат и переопределенности системы уравнений, что способствует повышению устойчивости вычислительных алгоритмов при их решении численными методами. Процедура формирования мате­матической модели полностью формализована и можно построить алгоритм ее реализации на ЭВМ.

Изложенная модификация узлового метода позволяет по­лучить модель в виде системы обыкновенных дифференциальных уравнений в нормальной форме Koшu, наиболее удобной при ис­пользовании численных методов интегрирования. Таким образом, эта модификация устраняет один из недостатков классического узлового метода.

Узловой метод хорошо приспособлен для моделирования электрических цепей, гидравлических и тепловых систем (движе­ние жидкости в гидравлических магистралях, теплопередача в твердом теле при одномерном тепловом потоке). Для механиче­ских систем он применим лишь в случае представления объектов в виде системы материальных точек или твердых тел, совершаю­щих простые движения — поступательные или вращательные.

Но узловой метод не может применяться для динамических систем, содержащих трансформаторные и фрикционные элемен­ты. Это обусловлено невозможностью отображения этих элементов матрицей инциденций. Узловым методом нельзя построить мате­матическую модель системы твердых тел при сложном их движе­нии — плоском, сферическом. Кроме того, в некоторых случаях для описания физических свойств технических объектов и взаи­модействия с внешней средой недостаточно использования рас­смотренных выше простых элементов. В частности, это относится к объектам с неголономными связями, с виртуальными связями и с переменной структурой. Такими свойствами обладают многие механические и гидромеханические системы.

Пример 4.2. Применим модифицированный узловой метод для формиро­вания математической модели анализа колебаний кузова автомобиля. Предполо­жим, что исследование колебаний осуществляется на основе динамической моде­ли, приведенной на рис. 4.5, а. Матрица инциденций для этого случая приведена в табл. 4.2. Используя ее, выпишем подматрицы ветвей источников , упругих 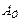и диссипативных ветвей:

; ; .

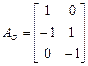Диагональные матрицы параметров элементов системы:

; ; .

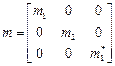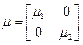Векторы потенциалов источников , упругих и диссипативных 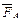компонентов:

; ; .

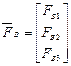И, наконец, необходимо составить вектор фазовых переменных типа пото­ка, необходимый для вычислений, предусмотренных вторым уравнением системы (4.20) и уравнением (4.21). Если объект подвержен внешним воздействиям только типа потенциала, то элементами этого вектора будут только независимые фазовые координаты 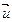. Если на объект действуют источники потока, то в элементный со­став вектора также включаются функции внешних воздействий 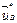. В этой связи вектор 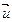в рассматриваемом примере имеет вид

где 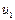и 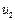— независимые фазовые координаты, определяющие состояния сосре­доточенных масс и ; 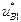— функция, характеризующая источник потока, воздействие которого на систему обусловлено неровностями опорной поверхности дороги.

Вычислим матричные произведения слагаемых правой части первого уравнения системы (4.20), принимая во внимание, что

.

После перемножения матриц получаем

; ;

.

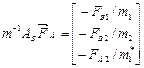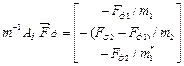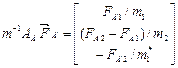Сложим полученные векторы, в соответствии с исходным уравнением:

.

Принимая во внимание, что , a 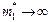, получаем два диф­ференциальных уравнения первого порядка и одно алгебраическое выражение, позволяющее определить реакцию внешней среды:

;

;

.

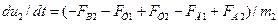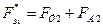Уравнения, необходимые для определения и , получим, вычислив матричные произведения в соответствии с выражениями (4.20) и (4.21):

;

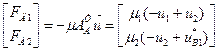
В результате математическая модель рассматриваемого объекта представ­ляется системой обыкновенных дифференциальных уравнений, общий порядок которой равен четырем, и тремя алгебраическими выражениями

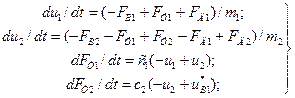(4.22)

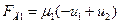; (4.23)

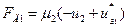; (4.24)

; (4.25)

Для решения системы уравнений (4.22) необходимо задать начальные ус­ловия , , , 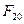. Значения и 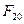обычно принимают исходя из ус­ловий статического равновесия: ; . Начальные скорости сосредоточенных масс 1>ю и и₂₀ можно принять нулевыми. Задавая функцию и решая уравнения (4.22) — (4.25), получают искомые значения фазовых переменных , , , , 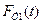а также реакцию опорной поверхности .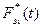

Если параметры элементов 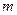, , 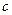рассматриваемой системы постоянны, то полученная математическая модель будет линей­ной. Однако в реальных системах значения параметров элементов зависят от фазовых координат и модель оказывается нелинейной. Так, в системах виброзащиты автомобилей коэффициенты жест­кости и 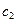могут быть функциями деформаций упругих элемен­тов. Кроме того, необходимо учитывать силы кулоновского тре­ния, являющиеся нелинейными функциями. Отметим, что силы кулоновского трения при составлении математической модели ус­ловно относят к внешним воздействиям.

В гидравлической системе используются нелинейные функ­ции для определения параметров диссипативных и упругих эле­ментов 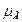и 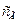(см. раздел 3.9).

Однако нелинейные функции не препятствуют построению математической модели узловым методом, так как они включают­ся в нее после формирования системы уравнений.

Date: 2016-07-18; view: 843; Нарушение авторских прав