
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Математическое моделирование случайных процессов
|
|
Классификация случайных процессов
Конкретная реализация процесса, описывающего случайного явления, называемого выборочной функцией или реализацией.
Будем понимать под случайным процессом конечную совокупность, другими словами, ансамбль реализации конечной длительности.
Рассмотрим ансамбль из N реализаций, определяющий некоторый случайный процесс: {xk(t)}, k=1,N

Вычислим путём усреднения по ансамблю среднее значение процесса в некоторый момент времени t1:
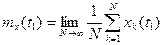
Получим корреляционную функцию случайного процесса, характеризующую взаимную зависимость его значений в различные моменты времени t1 и t1+τ:

Если mx(t1) и Kx(t1,t1+τ) не зависят от момента времени t1, т.е. mx(t1)=mx и Kx(t1,t1+τ)=Kx(τ), то случайный процесс называется стационарным.
Рассмотрим некоторую k-ю реализацию стационарного случайного процесса длительностью T.

Среднее значение и корреляционная функции этой реализации может быть получены путём усреднения по времени:

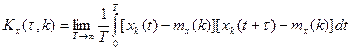
Если случайный процесс стационарен, а mx(k) и Kx(τ,k), вычислительные по различным реализациям совпадают, то случайный процесс называется эргодическим.
Для эргодических процессов характеристики, вычисленные усреднением по времени, равны аналогичными по ансамблю, т.е. mx(k)= mx. Kx(τ,k)= Kx
Таким образом все свойства эргодических процессов можно определить по единственной реализации.
Основные формы описания непрерывных случайных процессов
В большинстве практических задач моделирования систем для описания случайного процесса используются:
- ПРВ его значений x для фиксированного момента времени t, т.е. f(x,t);
- Корреляционная функция случайного процесса Kx(t1,t2), характеризующая взаимную зависимость его значений в различные моменты времени.
На основе ПРВ f(x,t) может быть определены любые средние характеристики или моменты распределения, в частности,
математическое ожидание 
дисперсия 
корреляционная функция Kx(t1,t2) формально определяется через двумерную ПРВ случайного процесса

причем при t1=t2=t имеем Kx(t1,t2)=Dx(t)
Для стационарного процесса
mx(t)=mx=const
Dx(t)=Dx=const,
а корреляционная функция становится функцией одного аргумента:
Kx(t1,t2)=Kx(t2,t1)=Kx(τ),
τ=t2-t1, Kx(0)=Dx
Для стационарного процесса вводится также функция спектральной плотности, как Фурье преобразование корреляционной функции.

где w - частоты случайных колебаний случайного процесса.
Соответственно имеют место соотношения
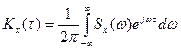

Таким образом, основными формами описания непрерывных процессов являются:
- распределения значений случайного процесса (f(x,t), mx(t), Dx(t),…) в конкретный момент времени;
- зависимости значений случайного процесса в различные моменты времени (Kx(t1,t2) или Kx(τ) и Sx(w) для стационарного процесса).
Получение на ЦВМ реализации случайного процесса с заданными коррелирующими свойствами
Реализация x(t) непрерывного случайного процесса с коррел. свойствами стационарного белого шума может быть получена на ЦВМ с помощью генератора случайных чисел в виде последовательности дискретных значений x(i*Dt), где i=0,1,2,…, Dt – период дискретизации времени
Стационарный случайный процесс с постоянной спектральной плотностью S0 называется стационарным белым шумом.
Его корреляционная функция 
где  - представление «дельта-функции» d(τ) интегралом Фурье.
- представление «дельта-функции» d(τ) интегралом Фурье.
Обычно корреляционная функция стационарного белого шума записывают в виде: Kx(τ)=G×d(τ), где G=S0=const – интенсивность стационарного белого шума
График корреляционной функции стационарного белого шума

Kx(0)=Dx
Kx(τ≠0)=0, так как s(t≠0)=0
График спектральной плотности
Как видно из графика корреляционной функции значения белого шума не зависит друг от друга (корреляция отсутствует)
Для получения реализации случайного процесса с заданной корреляционной функцией Kx(τ) используется специальные методы
1) Методы формирующего фильтра
Основан на использовании закономерностей преобразования линейным динамическим звеном (ЛДЗ) спектральной плотности случайного сигнала:
Sx(w)=|Ф(jw)|2Sg(w)
где Sx – спектральная плотность выходного сигнала
Sg - спектральная плотность входного сигнала
Ф(jw) – частотная передаточная функция ЛДЗ
Формирующим фильтром называется такое динамическое звено, которое обеспечивает требуемые корреляционные свойства выходного сигнала, т.е. задана спектральная плотность Sx(w)
Модель случайного процесса с заданными корреляционными свойствами можно построить на основе формирующего фильтра (ФФ), используя в качестве входного сигнала белый шум. В этом случае требуемая передаточная функция ФФ определяется из соотношения:

ФФ представляется ДУ ЛДЗ и добавляется к исходной математической модели случайного воздействия. В случае численного интегрирования на ЦВМ полученной таким образом системы ДУ случайное воздействие, задаваемое в форме реализации x(t) непрерывного случайного процесса представляется в виде последовательности дискретных значений x(ih), где h – шаг интегрирования, i=0,1,2,… Другими словами происходит аппроксимация реализации непрерывного случайного процесса дискретной реализацией с периодом дискретизации Dt, равным шагу интегрирования h. Такая замена не является эквивалентной, поэтому требуется корректировка соотношении, по которому определяются передаточная функция ФФ. Для обоснования необходимых коррекции исходного соотношения рассмотрим корелляционную функцию  и спектральная плотность
и спектральная плотность  дискретного случайного процесса, аппроксимирующего непрерывный белый шум с интенсивностью G0. В силу того, что в течении периода дискретизации, которая = шагу интегрирования h дискретный процесс сохраняет своё значение
дискретного случайного процесса, аппроксимирующего непрерывный белый шум с интенсивностью G0. В силу того, что в течении периода дискретизации, которая = шагу интегрирования h дискретный процесс сохраняет своё значение


Поэтому, если в качестве источника белого шума используется генератор случайных чисел с некоторым законом распределения, характеризуемым дисперсией Dx в соотношении в качестве спектральной плотности входного сигнала для ФФ следует брать значение:
S0= Dx *h
2) Метод скользящего суммирования
Основан на использовании интеграла свертки
 , где X(t) – реализация выходного сигнала – случайного сигнала с заданной корелляционной функцией
, где X(t) – реализация выходного сигнала – случайного сигнала с заданной корелляционной функцией
ξ(t) – реализация входного случайного сигнала (белого шума)
W(t) – весовая функция, которая определяется на основе обратного преобразования Лапласа передаточной функции формирующего фильтра
При моделировании интеграл свёртки реализуется в виде суммы:


Отметки i=0,1,2,3,4 на осях t соответствуют дискретным моментам времени ti=i*Dt, Dt – период дискретизации
Рассмотрим вычислительную процедуру метода с помощью временной диаграммы:
x(1)=W(0)* ξ(1);
x(2)=W(1)* ξ(1)+W(0)* ξ(2)
Вычислительная трудоёмкость метода значительно выше трудоемкости метода ФФ. Однако, метод ФФ реализуем только в случаях, когда КФ моделирования случайного процесса позволяет получить передаточную функцию ФФ. Метод же скользящего суммирования отличается универсальностью, поскольку весовая функция может быть получена при любой КФ, даже если соответствующий ФФ в форме динамического звена физически не реализуем.
В этом случае:
1) в расчетную формулу вместо несущ-й весовой функции W(τ) подставляют КФ Kx(τ):
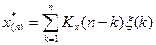
2) вычисляют математическое ожидание mx* и Dx* полученной реализации x*(n) случайного процесса, а также масштабный коэффициент  , оценивающий степень несовпадения W(τ) и Kx(τ).
, оценивающий степень несовпадения W(τ) и Kx(τ).
3) производят коррекцию полученной реализации x*(n) случайного процесса путём уменьшения центрированной составляющей
(x*(n)-mx*) в  раз, т.е. пропорционально отношению средне-квадратических отклонений полученной и искомой реализаций. В результате получается искомая реализация x(n) случайного процесса с заданной КФ Kx(τ) произвольного вида
раз, т.е. пропорционально отношению средне-квадратических отклонений полученной и искомой реализаций. В результате получается искомая реализация x(n) случайного процесса с заданной КФ Kx(τ) произвольного вида
Основные понятия исследования операций и системного анализа. Классификация задач исследования операций и принятия решений. Примеры формализации задач принятия решений.
Источник: лекция Кругликова «Исследования операций»
Исследование операций.
Сложная задача делится на этапы, каждый из которых решается как отдельная задача.
Системный подход
В соответсвии какому-то случайному объекту ставили систему, т.е. выделили данный объект. Всё, что внутри системы – элементы; за пределами системы – внешняя среда.
Система – совокупность взаимосвязанных элементов
- Определить границы системы, т.е. нужно сформулировать цель данной системы.
Система характеризуется состоянием S-вектор, набор отдельных показателей состояний.
S={S1, S2, … Sn}
Системы делятся на статические и динамические. Динамическая система изменяет своё состояние во времени. Для системы: автономные и неавтономные.
Автономная динамическая система S(t)
Неавтономная динамическая система может управлятся извне. U – вектор управляющих воздействий. S(t+dt)=Z[S(t), U(t)]
оператор
Системы: детерминированные и вероятностные (стохастические)
Модели:
- Статические
- Динамические
- Детерминированные
- Вероятностные
i. Дискретные
ii. Непрерывные

1) S={S1,S2, … Sn}

размерность
2) линейные / нелинейные
Пример:
(a) Плата с 6 микросхемами (самая простая модель)
- нужно уменьшить длину проводников. Число сочетаний расположения микросхем на плате:

Длина проводников:
 -соединение напрямую
-соединение напрямую
- определить коэффициенты связности между микросхемами.
Матрица размерностью 12´3 шаг Dx=2, Dy=1
(б) f(x) – функция
max -?
Многокритериальные задачи принятия решений. Варианты постановки и методы решения многокритериальных задач.
Источник: лекция Кругликова «Исследования операций»
1. Стоимостной критерий
2. Критерий технической эффективности
3. Надежность
4. Экологичность
5. Утилизация
Метод экспертных оценок
W1, W2, …, Wk
W(x) = a1W1(x)+…+ akWk(x) – обобщение

z1, z2, … zS – средние значения (оценка)
Метод уступок
W1(x), W2(x), …, Wk(x)
 Wc(x1, x2) – стоимость
Wc(x1, x2) – стоимость
Wn(x1, x2) – производительность
(x1, x2) Î D

 точка B – более эффективна точки А по обоим
точка B – более эффективна точки А по обоим
точка С – также эффективнее точки А критериям
Выделим область, на границе которых точки лучше, чем внутри области. Множество этих точек называется множеством Парето (среди них нужно искать оптимальное решение)
- Wc(x1, x2) – Min
(x1, x2) Î D
Решение: (x1*, x2*, Wc*)
Делаем уступку: Wc= Wc*+D Wc (чтобы повысить производительность)
- Wc(x1, x2) – Max
(x1, x2) Î D
Дополнительное условие: Wc(x1, x2) - Wc* £ D Wc
(x1*, x2*, Wп*)
Недостаток: отсутствие объективности в выборе величины уступки
Задача целочисленного программирования:
- W(x) – Max
x Î D
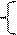 gi(x) £ bi, i=1,2,…m
gi(x) £ bi, i=1,2,…m
x³0
(x*, W*)
округление [x*]=x’ W’=W(x’)
Пример:
(1)
|
 5x1+7x2 £ 35 x1 ³ 0
5x1+7x2 £ 35 x1 ³ 0
(2) 4x1+9x2 £ 36 x2 ³ 0

Линия уровня: W(x1, x2) = const
0) x1=3,6 - нулевое приближение
x2=2,3
W*= 14,5
Решение не удовлетворяет условиям целочислинности
Дополнительные ограничения: x1 £ 3, x1 ³ 4
x2 £ 2, x2 ³ 3 =>
задача разветвилась на 2
1) x2 ≤ 2 => x1*=4,2 x2*=2
2) x2 ³ 3
3) x1 £ 4 => x1*=4 x2*=2 W*=14
4) x1 ³ 5 => x1*=5 x2*=1,3 W*=14,2

Max W(x1, x2)
{x1, x2}Î D
x1, x2 ³ 0
x1, x2 – целые
| W | x1 | x2 | ||
| 14,5 | 3,6 | 2,3 | x1=4 x2=2 W=14 | |
| 14,4 | 4,2 | 2,0 | x2 ≤ 2 | |
| 13,5 | 2,3 | 3,0 | x2 ³ 3 | |
| 14,0 | 4,0 | 2,0 | x1 ≤ 4 * | |
| 14,3 | 5,0 | 1,4 | x1 ³ 5 | |
| 13,3 | 2,0 | 3,1 | x1 ≤ 2 | |
| решения нет | x1 ³ 3 |
Задача о рюкзаке:
1 – положили предмет
0 – положили предмет
Важна ценность, которая должна быть Max, и вес груза
W(x1, x2) = 0,32x1+x2
(1) 2,3x1+10x2 £ 49,5
A(2,8; 4,3)
(2) 21x1+8,4x2 £ 9,5
B(3,4) Ï D
C(3,3); 3,96
D(2,4); 4,64
[1] Некоторые операторы языка ассемблера, например, такие, как операторы ввода/вывода, отображаются в несколько машинных команд.
[2] Название метода раскрутки произошло от фразы “to pull oneself up by one’s bootstrap”, т.е. "вытянуть себя за шнурки", аналогично легендарному методу барона Мюнхгаузена
Date: 2016-05-25; view: 1214; Нарушение авторских прав