Метод обратных функций

Этот метод получения заданного закона распределения основан на использовании известного результата теории вероятностей: независимо от вида непрерывного закона распределения при известной ФРВ F(x) случайная величина ξ=F(x) распределена по равномерному закону в интервале [0,1].

Если удаётся получить аналитическое выражение для функции F^-1(ξ), обратной ФРВ F(x), процедура генерирования случайных чисел x_i, будет выглядеть след. образом:

a) с помощью стандартного генератора получают равномерное распределение в интервале [0,1] числа ξ_i.

b) числа x_i получают по формуле x_i=F^-1(ξ_i), т.е. из соотношения F(x_i)= ξ_i

Рассмотренный способ позволяет, если только существует аналитическое выражение для F(x) и м.б. получена в аналитическом виде обратная функция.

Пример.

Получить значения x_i при ξ_i=0,1, если ПРВ определена на интервале , где a=2, b=10,2.

1) получим

2) получим x_i: F(x_i)= ξ_i =>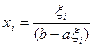

следовательно, x_i =0,01.

Способы построения генераторов нормального закона

Стандартизованным нормальным распределением называется нормальное распределение некоторой случайной величины U с нулевым математическим ожиданием и единичной дисперсией.

Связь любой случайной величины x с нормальным законом распределения и стандартной U выражается следующим соотношениями:

x=m_x+Uσ_x

где m_x и σ_x² - математическое ожидание и дисперсия случайной величины x.

Простейший способ получения случайной величины с нормальным законом распределения основан на центральной предельной теореме. В соответствии с ней среднее арифметическое n равномерно распределенных в интервале [0,1] случайных чисел имеет асимптотически нормальный закон распределения с математическим ожиданием 0,5 и дисперсией

На практике это в достаточной степени подтверждается при n=12.

Поэтому процедура получения нормального закона выглядит следующим образом:

а) с помощью стандартного генератора получают 12 равномерно распределенных в интервале [0,1] чисел ξ_i

б) числа x_j со стандартным нормальным законом распределения получают по формуле:

Диапазон возможных значений: [-6;+6]

Отметим, что рассмотренным способом не обеспечивается свойственный нормальному закону неограниченный диапазон распределения генерируемых чисел. От указанного недостатка свободна, например, следующая процедура:

а) с помощью стандартного генератора получают два равномерно распределенных в интервале [0,1] числа ξ_i и ξ_i+1;

б) вычисляют V₁=2 ξ_i-1; V2=2 ξ_i+1-1; S=V₁²+V₂²;

в) если S≥1, повторяют пункты а) и б);

г) вычисляют и получают два распределенных по стандартному нормальному закону числа x_j=V₁*r, x_j+1=V₂*r;

Метод Неймана

Это универсальный способ построения генератора случайных чисел с заданной ПРВ усеченного закона распределения, когда f(x)=0 за пределами [x_min, x_max].

Метод предусматривает следующие процедуры обеспечения заданной ПРВ f(x):

а) с помощью стандартного генератора получают пары равномерно распределенных в интервале [0,1] чисел ξ_2i-1 и ξ_2i

б) выполняют их преобразование

x_i=x_min+(x_max-x_min) ξ_2i-1

y_i=f_max ξ_2i, f_max – max значение ПРВ;

в качестве генерируемых значений случайной величины x выбирают значения x_i из тех пар x_i и y_i, для которой выполняется неравенство y_i≤f(x_i)

Date: 2016-05-25; view: 485; Нарушение авторских прав