Теоретические основы метода статистического моделирования

Метод СМ основывается на предельных теоремах теории вероятности.

1) Теорема Бернулли

Если проводится n независимых опытов в однородных условиях, в каждом из которых некоторое событие А осуществляется с вероятностью Р_А, то относительная частота появления события при сходится по вероятности Р_А, т.е. при любом e>0.

, где n_A – число положительных исходов опытов.

2) Теорема Пуассона

Если проводится n независимых опытов и вероятность осуществления события A в i-том опыте равна P_i, то h_n при сходится по вероятности к среднему из вероятностей P_i, т.е. при любом e>0.

3) Теорема Чебышева

Если в n независимых испытаниях наблюдаются значения СВ X, то при средних арифметических значений СВ сходится по вероятности к её мат. ожиданию , т.е. при любом e>0.

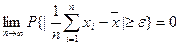
4) Обобщенная теорема Чебышева

Если - независимая СВ с мат. ожиданием и дисперсиями , ограниченными сверху одним и тем же числом, то

5) Центральная предельная теорема

Если - независимые одинаково распределенные СВ, имеющие мат. ожидание и дисперсию , то при закон распределения суммы неограниченно приближается к нормальному:

, где - интеграл вероятностей (специальная функция, для вычисления которого используются таблицы);

U – Стандартизованная нормальная случайная величина с ПРВ , т.е. с нулевым мат. ожиданием и единичной дисперсией

6) Частный случай ЦПТ (теорема Лапласа)

Если в каждом из n независимых опытов событие А появляются с вероятностью Р_А, то

Следствия:

а) При проведении независимых опытов в однородных условиях, в каждом из которых некоторое событие А осуществляется с вероятностью Р_А, последовательность относительных частот h_n имеет асимптотически нормальное распределение с мат. ожиданием и дисперсией

б) Если проведены n независимых опытов в однородных условиях, то последовательность СВ ,где - результаты отдельных опытов, имеет асимптотически нормальное распределение с мат. ожиданием и дисперсией , где и - мат. ожидание и дисперсия результатов {x_n} опытов (т.е. СВ, представленной случайной выборкой из n реализаций).

Date: 2016-05-25; view: 457; Нарушение авторских прав