Основные подходы к построению математических моделей систем управления

Рассмотрим структуру многомерной системы управления общего вида.

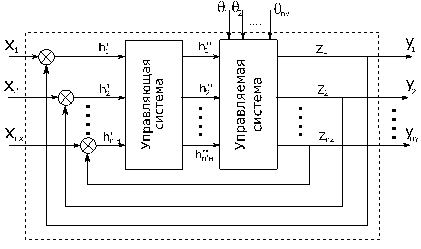
Независимые переменные:

- вектор входных (задающих) воздействий

- вектор возмущающих воздействий

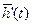- вектор сигналов ошибки

- вектор управляющих воздействий

Зависимые переменные:

- вектор состояний систем управления

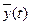- вектор выходных переменных

Для большинства систем управления:

При этом целью функционирования является изменение переменной 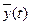согласно заданному закону с допустимой ошибкой.

Процесс функционирования системы описывается во времени оператором F, которое в общем случае преобразует независимые переменные в зависимые:

где 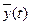- совокупность y_j(t) зависимостей выходных характеристик от времени для всех видов 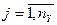, которые называются выходной траекторией.

Соотношения являются мат. описанием поведения объекта во времени, т.е. отражают его динамические свойства. Поэтому мат. модели такого вида принято называть динамическими.

1) В ряде случаев полная траектория движения системы может быть разбита на отдельные фазы, на которые свойства системы сохраняются неизменными. Такие фазы можно трактовать как дискретные состояния системы на интервале модели (0,T] в виде последовательности из смен. При этом отдельные состояния могут быть интерпретированы как координаты точки в К-мерном базовом пространстве:

, где 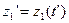, ,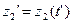…, в момент времени t’Î (0,T].

Состояния системы в момент времени 0<t*£T полностью определяются начальными условиями: 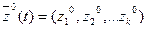где , ,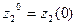…, ; входными воздействиями , внутренними переменными и воздействиями внешней среды , которые имели место за промежуток времени (t*-t₀), t₀=0, с помощью 2-х векторных уравнений:

Таким образом, цепочка уравнений объекта «вход – состояние – выход» позволяет определить характеристики системы:

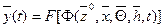
2) В общем случае время в модели системы может рассматриваться на интервале модели (0,T] как непрерывное, так и дискретное, т.е. квантованное на отрезке длиной Dt временных единиц каждый, когда T=m*Dt,где - число интервалов дискретизации.

3) В общем случае динамическая модель является стохастической. Но, если при описании объекта элементы случайности не учитываются, то выходные характеристики модели однозначно определяются детерминированными факторами.

Различные по характеру вскрываемых взаимосвязей модели стоятся по различным мат. схемам: непрерывно-детерминированной, дискретно-детерминированной, непрерывно-стохастической, дискретно-стохастической. Все перечисленные мат. схемы относятся к одному из 4-х подходов, используемых при построении моделей систем управления.