Формальное описание системы

Подготовка к исследованию мат. модели начинается с составления неформального описания системы. Неформальным описанием называется совокупность сведений, достаточная для установления алгоритма работы системы, т.е. построения её функциональной схемы. Описание схемы по её функциональной схеме с использованием определенного базиса операторов, позволяющих по входным воздействиям найти реакцию системы в общем виде, называется формальными.

Первым шагом формального описания системы является определение множества её параметров:

и базиса операторов:

где М – число звеньев системы, из которых состоит её функциональная схема.

Все параметры системы можно разбить на 4 множества:

(координаты системы)

где - фазовые переменные

- внешние параметры

- внутренние параметры

- выходные параметры

Фазовыми переменными системы называется функции времени V_i, которое определяют состояние системы в любой заданный момент времени.

В состав множества фазовых переменных входят:

- входные фазовые переменные образующие вектор входных воздействий

- выходные фазовые переменные, образующие вектор реакции системы

внутренние фазовые переменные

Оператор представляет собой правило, по которому каждому элементу x_i ставится в соответствие y_i. При этом имеет место соотношение: Y=AX

Внешними параметрами системы a называются физические величины, определяющие входные фазовые переменные X: X=X(a,t)

Внутренними параметрами системы b называются физические величины, определяющие свойства функционирования звеньев, описываемых операторами множества А:

X=X(a,t)

A=A(b)

…

С учетом этого система в наиболее общем виде может быть представлена уравнением:

Y(t)= A(b)X(a,t)

или схемой

Выходными параметрами системы g являются физические величины, определяющие качества работы системы. Для оценки выходных параметров формального описания системы в общем виде можно представить соотношением:

g=F₁(A₁,b,a)

где А - оператор, отображающий структуру системы.

Такое описание удается получить только в простейших случаях. При исследовании стохастических систем g получают в результате обработки реализаций выходной фазовой переменной Y, т.е. используют формальное описание вида

g = F₂[Y(t)]

где

T_н - время наблюдения реализации)

Пример: Составим формальное описание системы по следующей схеме:

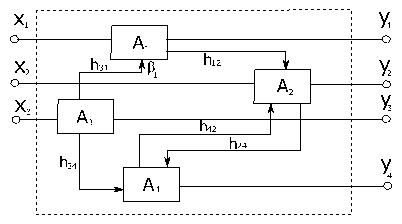
Y₁=A₁[b₁,X₁(a₁,t),h₃₁(t)];

Y₂=A₂[b₂,X₂(a₂,t),h₄₁(t),h₁₂(t)];

Y₃=A₃[b₃,X₃(a₃,t)];

Y₄=A₄[b₄,h₃₄(t),h₂₄(t)];

Формальное описание относительно выходной фазовой переменной Y₁:

Y₁=A₁[b₁,X₁(a₁,t); A₃[b₃,X₃(a₃,t)]];

Формальное описание относительно выходного параметра g₁, которое определяются только Y₁:

g₁=F2(Y1)=F2{ A₁[b₁,X₁(a₁,t); A₃[b₃,X₃(a₃,t)]] } - концептуальная модель

Date: 2016-05-25; view: 1400; Нарушение авторских прав