
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Для того чтобы спрогнозировать значение уровня ряда динамики по уравнению
|
|
Фурье, необходимо:
1. для значения  найти
найти  ,
,  ,
,  ;
;
2. по таблицам 14 – 16 найти  и
и  ;
;
Подставив значения тригонометрических функций в модель Фурье, получить прогнозное значение уровня ряда динамики.
Осуществляем прогноз. Январь, февраль и март 2009 года являются
Соответственно 13, 14 и 15 периодом от начала отсчета (январь 2008 года). Согласно результатам задач 13 и 14 получаем следующие прогнозы:
Январь:  (тыс. руб.);
(тыс. руб.);
Февраль:  (тыс. руб.);
(тыс. руб.);
Март:  (тыс. руб.).
(тыс. руб.).
Прогнозируем объем реализации по модели Фурье:
Январь:  ;
;  или
или
 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
m = 1:  (тыс. руб.);
(тыс. руб.);
m = 2: 
 (тыс. руб.);
(тыс. руб.);
m = 3: 

 (тыс. руб.);
(тыс. руб.);
Февраль:  ;
; 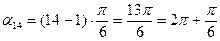 или
или
 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
m = 1: 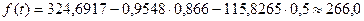 (тыс. руб.);
(тыс. руб.);
m = 2:  -
-
 (тыс. руб.);
(тыс. руб.);
m = 3: 

 (тыс. руб.);
(тыс. руб.);
Март:  ;
;  или
или
 ;
;  ;
;  ;
;
 ;
;  ;
; 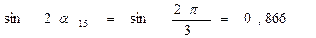 ;
;
 ;
;  ;
;  ;
;
m = 1:  (тыс. руб.);
(тыс. руб.);
m = 2:  -
-
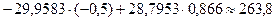 (тыс. руб.);
(тыс. руб.);
m = 3: 
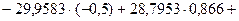
 (тыс. руб.).
(тыс. руб.).

Для заметок
Тема 5. «Экономические индексы»
Задача 18. Торгово – промышленное предприятие производит и реализует три вида товаров А, В и С. Его деятельность в 2007 – 2008 годах характеризовалась следующими данными:
| Товар | Себестоимость, руб./шт. | Цена изделия, тыс. руб./шт. | Объем выпуска, тыс. шт. | Время на производство единицы продукции, ч. | ||||
| А | 0,87 | 0,85 | 5,8 | 6,4 | 0,12 | 0,18 | ||
| В | 0,44 | 0,45 | 7,0 | 7,5 | 0,20 | 0,24 | ||
| С | 0,38 | 0,41 | 10,0 | 14,0 | 0,15 | 0,09 |
Необходимо:
а) найти индивидуальные индексы себестоимости, цены, объема, затрат и товарооборота;
б) вычислить сводные индексы себестоимости, цены, объема, затрат и товарооборота двумя способами (по определению и используя формулы средних);
в) определить величину экономии или перерасхода производителя от изменения себестоимости, а также экономию или перерасход покупателя от изменения цены.
1. Обозначим 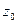 и
и  ,
,  и
и  ,
, 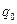 и
и  - соответственно себестоимость z, цена p и объем q (объем производства, продаж и т. д.) базисного и отчетного периодов.
- соответственно себестоимость z, цена p и объем q (объем производства, продаж и т. д.) базисного и отчетного периодов.
2. Индексом называется сложный относительный показатель, характеризующий изменение некоторого экономического признака. Индексы делятся на индивидуальные (рассматривающие изменения отдельных единиц совокупности) и сводные или агрегатные, измеряющие суммарное изменение показателей. Расчетные формулы для нахождения индексов себестоимости, цены, объема, затрат и товарооборота приведены в таблице:
| Наименование индекса | Индивидуальный | Сводный | |
| Определение | Средневзвешенная формула | ||
| Индекс себестоимости | 
| 
| 
|
| Индекс цены | 
| 
| 
|
| Индекс объема | 
| 
| 
|
| Индекс затрат |  или
или

|  или
или

| - |
| Индекс товарооборота |  или
или
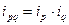
|  или
или

| - |
3. С помощью индексов можно найти величину экономии (отрицательное число) или перерасхода (положительное число) производителя от изменения себестоимости:
 .
.
4. Величина экономии (отрицательное число) или перерасхода (положительное число) потребителя от изменения цены равна:
 .
.
Все необходимые для решения задачи расчеты произведены в таблице 18.
На основании найденных индивидуальных индексов произведем анализ товара А. Имеем:
 или 121,17%;
или 121,17%;
 или 97,7%;
или 97,7%;
 или 110,34 %;
или 110,34 %;
 или 133,7%;
или 133,7%;
 или 107,81%.
или 107,81%.
Таблица 18
| Товар | 
| 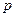
| 
| Расчетные графы | ||||||||
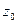
| 
| 
| 
| 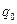
| 
| 
| 
| 
| 
| 
| 
| |
| А | 0,87 | 0,85 | 5,8 | 6,4 | 3993,6 | 5,44 | 5,568 | 5,046 | ||||
| В | 0,44 | 0,45 | 7,5 | 1822,5 | 1822,5 | 3,375 | 3,3 | 3,08 | ||||
| С | 0,38 | 0,41 | 5,74 | 5,32 | 3,8 | |||||||

| - | - | - | - | - | - | 8182,1 | 7610,5 | 14,555 | 14,188 | 11,926 |
Таблица 18 (продолжение)
| Товар | Расчетные графы | ||||||||||

| 
| 
| 
| 
| 
| 
| 
| 
| 
| ||
| А | 1,2117 | 0,9770 | 1,1034 | 1,3370 | 1,0781 | 0,8253 | 1,0235 | 5,568 | 5,568 | ||
| В | 1,0000 | 1,0227 | 1,0714 | 1,0714 | 1,0958 | 1,0000 | 1822,5 | 0,9778 | 3,3 | 3,3 | |
| С | 0,9494 | 1,0789 | 1,4000 | 1,3292 | 1,5105 | 1,0533 | 0,9268 | 5,32 | 5,32 | ||

| - | - | - | - | - | - | 7610,5 | - | 14,188 | 14,188 |
Себестоимость товара А в 2008 году по сравнению с 2007 годом увеличилась на 21,17%. Цена товара сократилась на 2,3%, а объем выпуска увеличился на 10,34%. Затраты на производство товара А в 2008 году по сравнению с 2007 годом увеличились на 33,7%. Товарооборот увеличился на 7,81%.
Переходим к расчету сводных индексов.
Индекс себестоимости
 или 107,51%.
или 107,51%.
К этому же результату приходим, находя сводный индекс себестоимости по среденевзвешенной формуле (см. таблицу 18):  . Итак, в среднем, себестоимость товаров А, В и С в 2008 году по сравнению с 2007 годом возросла на 7,51%.
. Итак, в среднем, себестоимость товаров А, В и С в 2008 году по сравнению с 2007 годом возросла на 7,51%.
Сводный индекс цены равен
 или 102,59%,
или 102,59%,
что говорит о среднем росте цен на товары в среднем на 2,59%. Тот же результат дает средневзвешенная формула:  .
.
Агрегатный индекс объема равен
 или 118,97%.
или 118,97%.
Его значение аналогично результату, полученному по средневзвешенной формуле:  . Итак, объем производства товаров вырос на 18,97%.
. Итак, объем производства товаров вырос на 18,97%.
Затраты в 2008 году по сравнению с 2007 годом возросли на 26,5%, а товарооборот – на 22,04%, поскольку
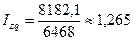 или 126,5%,
или 126,5%,
 или 122,04%.
или 122,04%.
За счет увеличения себестоимости и объема выпуска наблюдается перерасход производителя в размере
 (тыс. руб.).
(тыс. руб.).
Рост цен и объема производства повлек за собой перерасход потребителя в размере
 (млн. руб.).
(млн. руб.).
Задача 19. По данным задачи 18 необходимо:
а) вычислить индивидуальный индекс производительности труда;
б) определить сводный индекс производительности труда, взвешенный по трудоемкости;
в) найти сводный индекс производительности труда, взвешенный по выработке;
г) подсчитать средний индекс производительности труда, взвешенный по трудоемкости.
1. Обозначим  - время, необходимое на производство единицы продукции (трудоемкость). Тогда, суммарные затраты времени на производство всей продукции данного типа
- время, необходимое на производство единицы продукции (трудоемкость). Тогда, суммарные затраты времени на производство всей продукции данного типа
 .
.
Производительность труда таким образом может быть определена как отношение объема производства к затратам на производства это объема продукции или величина, обратная к трудоемкости:
 или
или  .
.
2. Индивидуальный индекс производительности труда равен:
 или
или  .
.
3. Сводный индекс производительности труда, взвешенный по трудоемкости может быть подсчитан двумя способами: по определению и по формуле средней арифметической взвешенной,
 .
.
4. Сводный индекс производительности труда, взвешенный по выработке, равен:
 ,
,
при этом 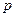 - сопоставимые цены, то есть цены отчетного, базисного или любого другого периодов, а также средние цены.
- сопоставимые цены, то есть цены отчетного, базисного или любого другого периодов, а также средние цены.
Составляем расчетную таблицу 19. В качестве сопоставимых цен используем средние цены, то есть
 .
.
Таблица 19
| Товар | 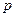
| 
| 
| Расчетные графы | |||||||

| 
| 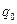
| 
| 
| 
| 
| 
| 
| 
| 
| |
| А | 0,87 | 0,85 | 5,8 | 6,4 | 0,12 | 0,18 | 0,696 | 1,152 | 8,3333 | 5,5556 | 0,6667 |
| В | 0,44 | 0,45 | 7,5 | 0,2 | 0,24 | 1,4 | 1,8 | 4,1667 | 0,8333 | ||
| С | 0,38 | 0,41 | 0,15 | 0,09 | 1,5 | 1,26 | 6,6667 | 11,1111 | 1,6667 | ||

| - | - | - | - | - | - | 3,596 | 4,212 | - | - | - |
Таблица 19 (продолжение)
| Товар | Расчетные графы | ||||||

| 
| 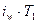
| 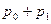
| 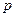
| 
| 
| |
| А | 0,768 | 1,152 | 0,768 | 1,72 | 0,86 | 4,988 | 5,504 |
| В | 1,5 | 1,8 | 1,5 | 0,89 | 0,445 | 3,115 | 3,3375 |
| С | 2,1 | 1,26 | 2,1 | 0,79 | 0,395 | 3,95 | 5,53 |

| 4,368 | 4,212 | 4,368 | - | - | 12,053 | 14,3715 |
Индивидуальные индексы производительности труда по каждому товару соответственно равны:
товар А,  = 0,6667 или 66,67%;
= 0,6667 или 66,67%;
товар В,  = 0,8333 или 83,33 %;
= 0,8333 или 83,33 %;
товар С,  = 1,6667 или 166,67 %.
= 1,6667 или 166,67 %.
Таким образом в первом случае производительность труда снизилась на 33,32%, во втором – на 16,67%, третьем производительность труда возросла на 66,67%.
Сводный индекс производительности труда, взвешенный по трудоемкости, равен
 или 103,7%.
или 103,7%.
Индекс производительности труда, взвешенный по выработке, равен:
 или 101,8%.
или 101,8%.
Согласно средневзвещенной формуле
 .
.
Задача 20. По рассчитанным значениям индексов цен переменного состава, фиксированного состава, а также индексов структурных сдвигов, произвести анализ реализации товара А в трех регионах. Цены на товар и объемы его реализации в 2007 – 2008 годах приведены в таблице:
| Регион | ||||
| Цена, у. е./ шт. | Продано, тыс. шт. | Цена, у. е./ шт. | Продано, тыс. шт. | |
| 7,80 | 7,90 | |||
| 8,00 | 8,15 | |||
| 7,65 | 7,70 |
1. Индекс цен переменного состава рассчитывается как отношение средних цен отчетного и базисного периодов:
 .
.
2. Изменение индивидуальных цен, а также изменение и специфика реализации (производства) в различных местах продажи (производства) учитывается индексом структурных сдвигов:
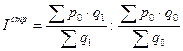 .
.
3. изменение цен без учета структуры производится с помощью индекса цен фиксированного состава, который рассчитывается также как и агрегатный индекс цен, введенный в задаче 18:
 .
.
4. между введенными индексами существует связь:
 .
.
Производим все необходимые расчеты:
| Регион | 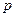
| 
| Расчетные графы | ||||

| 
| 
| 
| 
| 
| 
| |
| 7,8 | 7,9 | ||||||
| 8,15 | 774,25 | ||||||
| 7,65 | 7,7 | 887,4 | 902,7 | 908,6 | |||

| - | - | 2647,4 | 2832,7 | 2867,85 |
Имеем:
 или 101,16%;
или 101,16%;
 или 101,24%;
или 101,24%;
 или 99,92%,
или 99,92%,
или (осуществляем проверку) 1,0124*0,9992≈1,0116.
Видим, что средняя цена возросла на 1,16% в 2008 году по сравнению с 2007 годом. Однако, рассчитанный индекс цен фиксированного состава указывает на рост цен в размере 1,24%. Такое несоответствие произошло потому, что во втором случае не было учтено изменение структуры реализации: в 2008 году по более дорогой цене было продано меньше изделий, а по дешевой цене больше, чем в 2007 году. В целом же цены за счет изменения структуры снизились на 0,08%, что и привело к полученному росту в среднем на 1,16%.
Задача 21. По ценам и реализации товаров трех видов в двух регионах А и В рассчитать территориальный индекс цен двумя способами, а также индекс физического объема реализации.
| Товар | Регион А | Регион В | ||
| Цена, у. е./ шт. | Продано, тыс. шт. | Цена, у. е./ шт. | Продано, тыс. шт. | |
| 10,0 | 175,50 | 10,7 | 200,00 | |
| 14,0 | 38,45 | 14,2 | 40,04 | |
| 8,4 | 118,22 | 8,3 | 150,25 |
Date: 2016-05-25; view: 423; Нарушение авторских прав