Случайной величины, имеющее максимальную частоту

3. Для каждого значения х определяем условные варианты

.

4. Вычисляем условные моменты:

; ; ; .

5. Искомые значения рассчитываются по формулам:

;

;
;

.

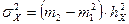Из группированного статистического ряда (см задачу 1) заключаем, что

= 1.

Так как максимальной частоте ряда 28 соответствует значение случайной величины 21,5 (см. группированный статистический ряд, задача 1), то

=21,5.

Отсюда, условный вариант

.

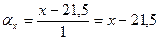Нахождение условных моментов удобно производить в таблице:

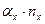
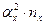
18,5		-3	-9		-81
19,5		-2	-22		-88
20,5		-1	-27		-27
21,5
22,5
23,5
24,5
25,5
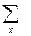
		-	-4

Тогда, условные варианты соответственно равны:

; ; ; .

Итак, требуемые величины соответственно равны:

;

; ;

.

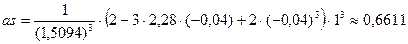Задача 6. Для выборки из задачи 1 с вероятностью γ = 0,95 определить границы интервала, в котором заключено математическое ожидание а (генеральная средняя или среднее значение генеральной совокупности) и сделать соответствующие выводы. Задачу решить в предположении а) повторного, б) бесповторного отбора из генеральной совокупности объема

N = 1500.

С доверительной вероятностью γ утверждается, что математическое ожидание а принадлежит интервалу:

,

где - выборочная средняя (среднее значение признака, рассчитанное по выборке), δ – предельная ошибка, равная

,

причем t – постоянная величина, значение которой определяется в зависимости от γ, в частности

t = 3, если γ =0,99,

t = 2, если γ =0,95,

t = 1, если γ =0,63,

μ – средняя ошибка выборки, равная

- если отбор случайный – повторный,

- если отбор случайный – бесповторный.

Имеем (см. задачу 4):

, , n = 100, N = 1500, t = 2.

Средняя ошибка выборки равна:

,

,

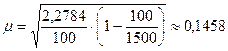Если отбор повторный или бесповторный соответственно. Тогда, в зависимости от типа отбора, предельная ошибка выборки равна:

или .

Получаем: нижняя граница доверительного интервала:

;

верхняя граница доверительного интервала:

.

Итак, с вероятностью 0,95 можно утверждать, что средний диаметр

детали, изготавливаемой предприятием находится в пределах от 21,1582 до

21,7618 мм (если выборка организована методом случайного повторного

отбора) и от 21,1684 до 21,7516 мм (если выборка случайная, бесповторная).

Задача 7. Для выборки из задачи 1 с вероятностью γ = 0,99 определить

границы интервала, в котором заключена генеральная доля признака р –

диаметр детали, находящийся в пределах от 20 до 23 мм включительно и

сделать соответствующие выводы. Задачу решить в предположении

бесповторного отбора из генеральной совокупности объема N = 2000.

С доверительной вероятностью γ утверждается, что математическое ожидание р принадлежит интервалу:

,

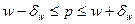где 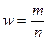- выборочная доля ( m – количество элементов выборочной совокупности, обладающих интересующим нас признаком, n – объем выборочной совокупности), – предельная ошибка доли, равная

,

причем t – постоянная величина, значение которой определяется в зависимости от γ также, как и в задаче 6, – средняя ошибка доли, равная

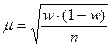- если отбор случайный – повторный,

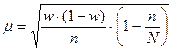- если отбор случайный – бесповторный.

В выборке интересующий нас диаметр детали (от 20 до 23 мм) принадлежит интервалам (см. задачу 1) (20;21), (21;22) и (22;23), частоты которых соответственно равны 27, 28 и 19. Следовательно, выборочная доля

.

Согласно условию задачи находим предельную ошибку доли:

.

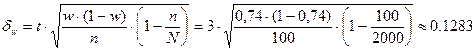Имеем: нижняя граница доверительного интервала:

;

верхняя граница доверительного интервала:

.

Итак, с вероятностью 0,99 утверждается, что среди 2000 деталей доля деталей диаметра от 20 до 23 мм находится в пределах от 0,6117 до 0,8683 (от 61,17% до 86,83%).

Для заметок

Тема 2. «Проверка статистических гипотез»

Задача 8. С вероятностью 0,95 проверить гипотезу о том, что генеральная

совокупность, которой принадлежит выборка из задачи 1, распределена по

нормальному (Гауссову) закону распределения случайной величины.

Гипотеза о нормальном распределении генеральной совокупности,

которой принадлежит исследуемая выборка, с доверительной вероятностью

γ проверяется с помощью - критерия согласия Пирсона (критерия хи –

квадрат). Приведем алгоритм проверки гипотезы с помощью этого критерия.

Date: 2016-05-25; view: 567; Нарушение авторских прав