Степень влияния факторного признака X на результативный признак Y определяется с помощью индекса детерминации

.

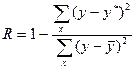9. Величины средней ошибки аппроксимации и индекса детерминации позволяют определить наиболее точную регрессионную модель. Ей считается та, у которой одновременно средняя ошибка аппроксимации стремится к минимуму, а индекс детерминации – к максимуму,

, .

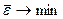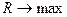10. Прогноз значения у происходит путем подстановки данного значения х в уравнение регрессии у на х. Аналогично, для прогноза значения х по заданному значению у, необходимо использовать уравнение регрессии х на у.

Таблица 10

	у на х	х на у
Линейная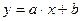
,	,
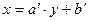
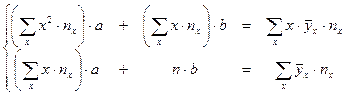
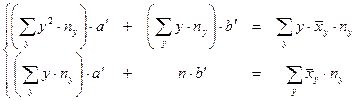
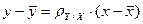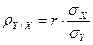
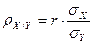
Параболическая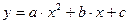
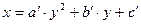
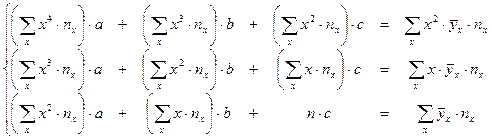
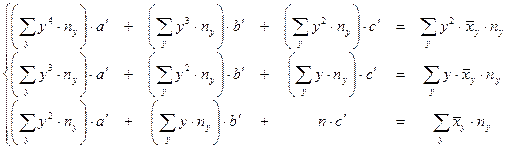
Показательная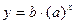

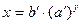
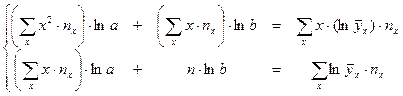
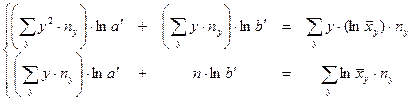
Переходим к решению задачи. Вначале запишем исходные данные в виде корреляционной таблицы:

Х Y	(5;9)	(9;13)	(13;17)	(17;21)	(21;25)	(25;29)
(1;3)
(3;5)
(5;7)
(7;9)
(9;11)
(11;13)
(13;15)

Строим корреляционное поле данных (рисунок 10)

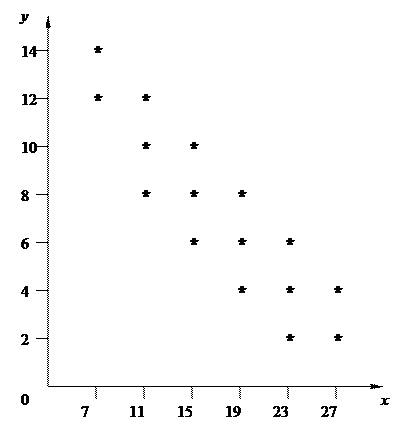
Рис. 10

Производим все необходимые вычисления в ниже приведенной таблице. В клетке, стоящей на пересечении строки 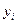и столбца указаны следующие данные:

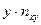
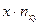
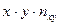
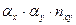
X Y	(5;9)	(9;13)	(13;17)	(17;21)	(21;25)	(25;29)
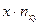
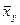
-2	-1
(1;3)		-1																					26,1111
														-4			-21
(3;5)																							22,6364
(5;7)
(7;9)
					-2
(9;11)
					-18
(11;13)																							8,333
		-16			-4
(13;15)
		-50
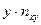
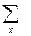
	13,4286		7,2	5,25	3,7143	2,6	-
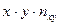
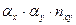
	-66	-24			-2	-21	-108
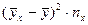
	307,5657	81,92	1,6	19,22	66,6514	176,4	653,3571
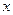
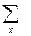
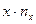
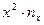
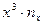
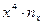
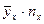
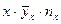
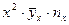
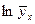
	2,5974	2,3026	1,9741	1,6582	1,3122	0,9555	-
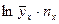
	18,1817	18,4207	19,7408	13,2658	9,1853	9,5551	88,3494
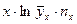
	127,2718	202,6275	296,1122	252,0507	211,2620	257,9881	1347,3123

у
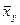
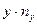
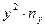
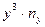
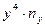
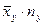
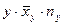
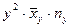
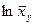
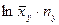
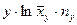
		26,1111								3,2624	29,3612	58,7225
		22,6364								3,1196	34,3151	137,2605
										2,8332	28,3321	169,9928
										2,7081	10,8322	86,6576
										2,4849	19,8793	198,7925
		8,333								2,1203	6,3608	76,3295
										1,9459	9,7296	136,2137
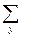
		-								-	138,8103	863,9692

Строим эмпирические линии (рисунок 11; на нем сплошной линией изображена эмпирическая линия регрессии у на х, а пунктирной – эмпирическая линия регрессии х на у) регрессии и делаем первоначальные выводы о форме корреляционной зависимости.

Рис. 11

Так как с ростом значения х значения у почти монотонно убывают, то скорее всего имеет место линейная обратная корреляционная зависимость.

Определим величину коэффициента линейной корреляции. Среднее значение признаков найдем согласно определению, а дисперсии рассчитаем по формуле разностей. Имеем:

;

;

;

;

;

;

;

.

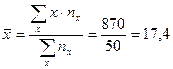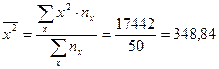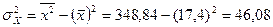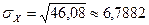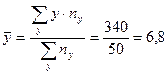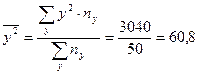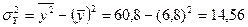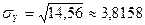Среднее значение произведения

.

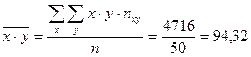Тогда числитель коэффициента линейной корреляции, рассчитанный первым способом, равен:

.

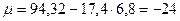Найдем величину μ методом моментов. Используя соответствующие определения и расчетную таблицу, получаем:

.

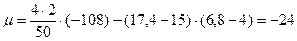Итак, коэффициент линейной корреляции равен:

,

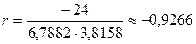что говорит о том, что рассматриваемая зависимость является линейной обратной.

Переходим к вычислению корреляционного отношения. Межгрупповая дисперсия равна

,

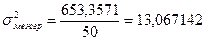отсюда

;

.

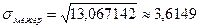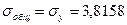Итак, корреляционное отношение равно

.

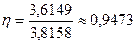Найденное значение говорит о тесной корреляционной зависимости между рассматриваемыми признаками.

Проверим с вероятностью 0,95 гипотезу о статистической значимости эмпирических данных. Наблюдаемое значение критерия Стьюдента равно.

.

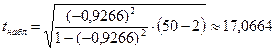Критическое значение находим по таблице 3 приложения для уровня значимости α = 1-0,95=0,05 и числа степеней свободы ν = 50 – 2= 48:

.

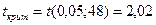Имеем:

17,0664>2,02,

следовательно гипотеза о статистической значимости эмпирических данных принимается с указанной вероятностью.

Находим параметры регрессионных моделей (см. таблицу 10). Результаты вычислений представим в таблицах:

Линейная корреляционная зависимость
Система нормальных уравнений	у на х	Система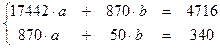
Решение системы	,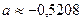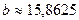
Уравнение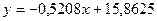
х на у	Система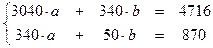
Решение системы	,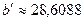
Уравнение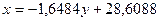
Упрощенный способ	у на х	ρ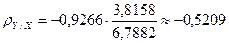
Уравнение	,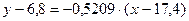
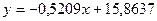
х на у	ρ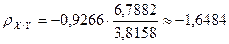
Уравнение	,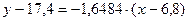

Параболическая корреляционная зависимость
у на х	Система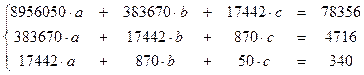
Решение системы	, ,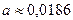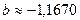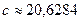
Уравнение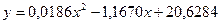
х на у	Система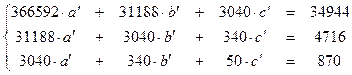
Решение системы	, ,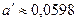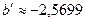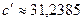
Уравнение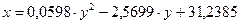
Показательная корреляционная зависимость
у на х	Система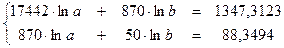
Решение системы	, , ,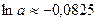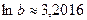
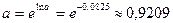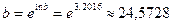
Уравнение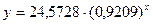
х на у	Система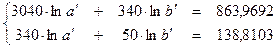
Решение системы	, , ,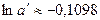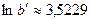
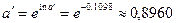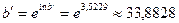
Уравнение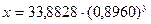

По каждой из полученных моделей находим величину средней ошибки аппроксимации и индекса детерминации (расчеты приведены в таблице 11). Имеем: для линейной модели

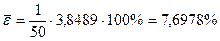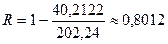, или 80,12%;

для параболической модели

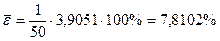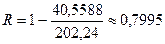, или 79,95%;

для показательной модели

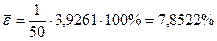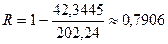, или 79,06%.

Видим, что одновременно минимум средней ошибки аппроксимации и максимум индекса детерминации соответствует линейной регрессионной модели. Следовательно, она признается наиболее точной.

Графики линейной зависимости приведены на рисунке 12, параболической – на рисунке 13, а показательной – на рисунке 14. На них сплошной чертой изображены линии регрессии у на х, а пунктирной – х на у.

Строим прогноз признаков. Имеем: при стоимости основных производственных фондов 2,5 млн. руб., затраты на капитальный ремонт составят

(%).

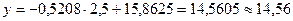Если затраты на капитальный ремонт составляют 0,52% от ОПФ, то стоимость основных производственных фондов должна составлять

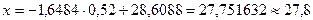(млн. руб.)

Таблица 11

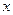
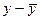
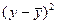
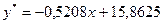
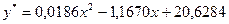
у				Линейная модель	Параболическая модель	Показательная модель
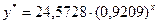
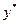
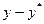
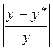
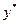
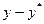
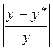
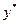
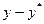
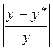
		-4,8	23,04	3,8833	-1,8833	3,5469	0,9417	3,6100	-1,6100	2,5922	0,8050	3,6887	1,6887	2,8515	0,8443
	-4,8	23,04	1,8000	0,2000	0,0400	0,1000	2,6556	-0,6556	0,4298	0,3278	2,6524	0,6524	0,4256	0,3262
		-2,8	7,84	5,9667	-1,9667	3,8678	0,4917	5,1586	-1,1586	1,3424	0,2897	5,1298	1,1298	1,2764	0,2824
	-2,8	7,84	3,8833	0,1167	0,0136	0,0292	3,6100	0,3900	0,1521	0,0975	3,6887	-0,3113	0,0969	0,0778
	-2,8	7,84	1,8000	2,2000	4,8400	0,5500	2,6556	1,3444	1,8074	0,3361	2,6524	-1,3476	1,8161	0,3369
		-0,8	0,64	8,0500	-2,0500	4,2025	0,3417	7,3014	-1,3014	1,6935	0,2169	7,1340	1,1340	1,2859	0,1890
	-0,8	0,64	5,9667	0,0333	0,0011	0,0056	5,1586	0,8414	0,7079	0,1402	5,1298	-0,8702	0,7572	0,1450
	-0,8	0,64	3,8833	2,1167	4,4803	0,3528	3,6100	2,3900	5,7120	0,3983	3,6887	-2,3113	5,3423	0,3852
		1,2	1,44	10,1333	-2,1333	4,5511	0,2667	10,0383	-2,0383	4,1545	0,2548	9,9212	1,9212	3,6911	0,2402
	1,2	1,44	8,0500	-0,0500	0,0025	0,0062	7,3014	0,6986	0,4881	0,0873	7,1340	-0,6660	0,7500	0,1083
	1,2	1,44	5,9667	2,0333	4,1344	0,2542	5,1586	2,8414	8,0735	0,3552	5,1298	-2,8702	8,2381	0,3588
		3,2	10,24	10,1333	-0,1333	0,0178	0,0133	10,0383	-0,0383	0,0015	0,0038	9,9212	-0,0788	0,0062	0,0079
	3,2	10,24	8,0500	1,19500	3,8025	0,1960	7,3014	2,6986	7,2827	0,2699	7,1340	-2,8660	8,2140	0,2866
		5,2	27,04	12,2167	-0,2167	0,0469	0,0181	13,3693	-1,3693	1,8751	0,1141	13,7974	1,7974	3,2307	0,1498
	5,2	27,04	10,1333	1,8667	3,4844	0,1556	10,0383	1,9617	3,8484	0,1635	9,9212	-2,0788	4,3213	0,1732
		7,2	51,84	12,2167	1,7833	3,1803	0,1274	13,3693	0,6307	0,3977	0,0450	13,7974	0,2026	0,0410	0,0145
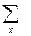
	-	-	202,24	-	-	40,2122	3,8489	-	-	40,5588	3,9051	-	-	-	3,9261

Рис. 12

Рис. 13

Рис. 14

Задача 10. Имеются следующие показатели по десяти предприятиям некоторой отрасли (на 31.12.2007):

Приняв стоимость основных промышленно – производственных основных фондов за результативный признак, а остальные показатели – за факторные признаки, необходимо:

а) исключив один из факторных признаков, перейти к двухфакторной регрессии;

б) вычислить множественный коэффициент корреляции и сделать выводы о форме и силе корреляционной зависимости;

в) с помощью F – критерия Фишера с вероятностью 0,95 оценить статистическую значимость эмпирических данных;

г) вычислить значение общего индекса детерминации;

д) двумя способами получить уравнение линейной модели множественной регрессии;

е) по величине средней ошибки аппроксимации оценить точность линейной модели;

ж) подсчитать дельта – коэффициенты;

з) найти значения коэффициентов эластичности;

и) исключить из модели один из факторных признаков и перейти к модели с парной регрессией.

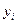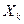1. Эмпирические данные выборки объема n принято записывать в виде таблицы, в которой Y – результативный признак со значениями , а , ,…, - факторные признаки со значениями 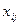, i=1,2,…, n, j=1,2,… k:

	Y			…
				…
				…
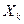
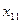
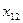
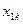
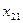
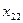
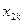
n				…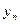

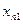
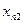
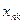
Date: 2016-05-25; view: 575; Нарушение авторских прав